P1038 [NOIP 2003 Senior] Neural Network

人工神经网络（Artificial Neural Network）是一种新兴的具有自我学习能力的计算系统，在模式识别、函数逼近及贷款风险评估等诸多领域有广泛的应用。对神经网络的研究一直是当今的热门方向，兰兰同学在自学了一本神经网络的入门书籍后，提出了一个简化模型，他希望你能帮助他用程序检验这个神经网络模型的实用性。

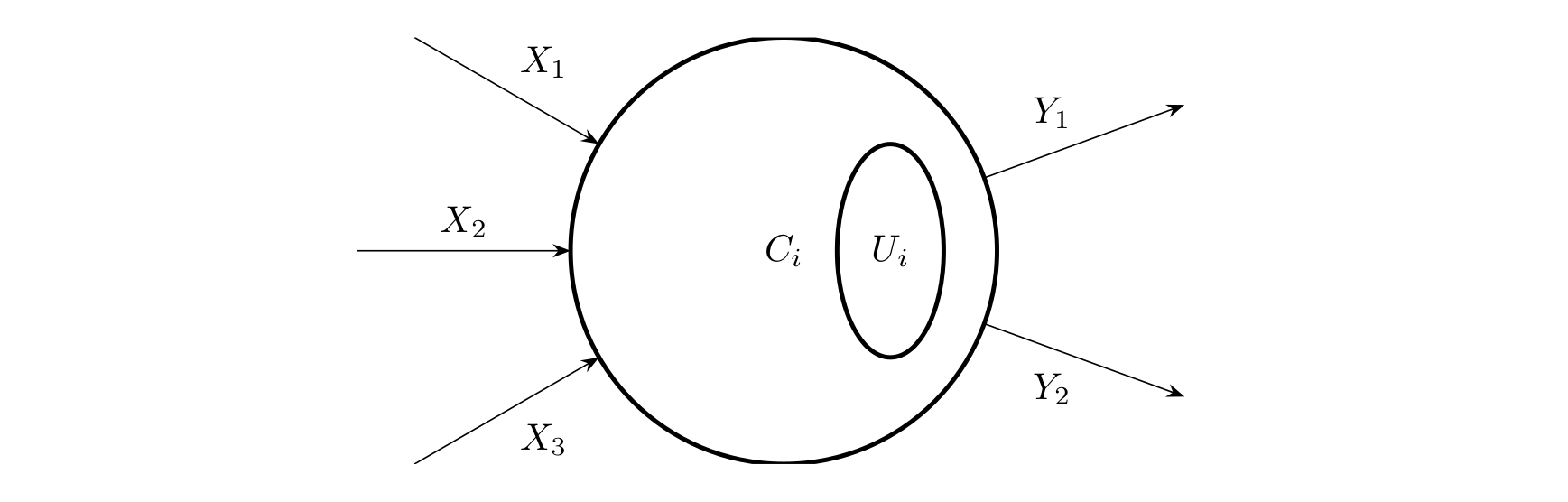
In Lanlan’s model, a neural network is a directed graph whose nodes are called neurons, and there is at most one edge between any two neurons. The figure below shows an example of one neuron.  Neuron (index $i$). In the figure, $X_1 \sim X_3$ are input channels, $Y_1 \sim Y_2$ are output channels, $C_i$ is the current state of the neuron, and $U_i$ is the threshold, which can be regarded as an intrinsic parameter of the neuron. Neurons are arranged in order to form the entire neural network. In Lanlan’s model, neurons are divided into multiple layers: the input layer, the output layer, and several intermediate layers. Each layer only outputs information to the next layer and only receives information from the previous layer. The figure below shows a simple three-layer neural network.  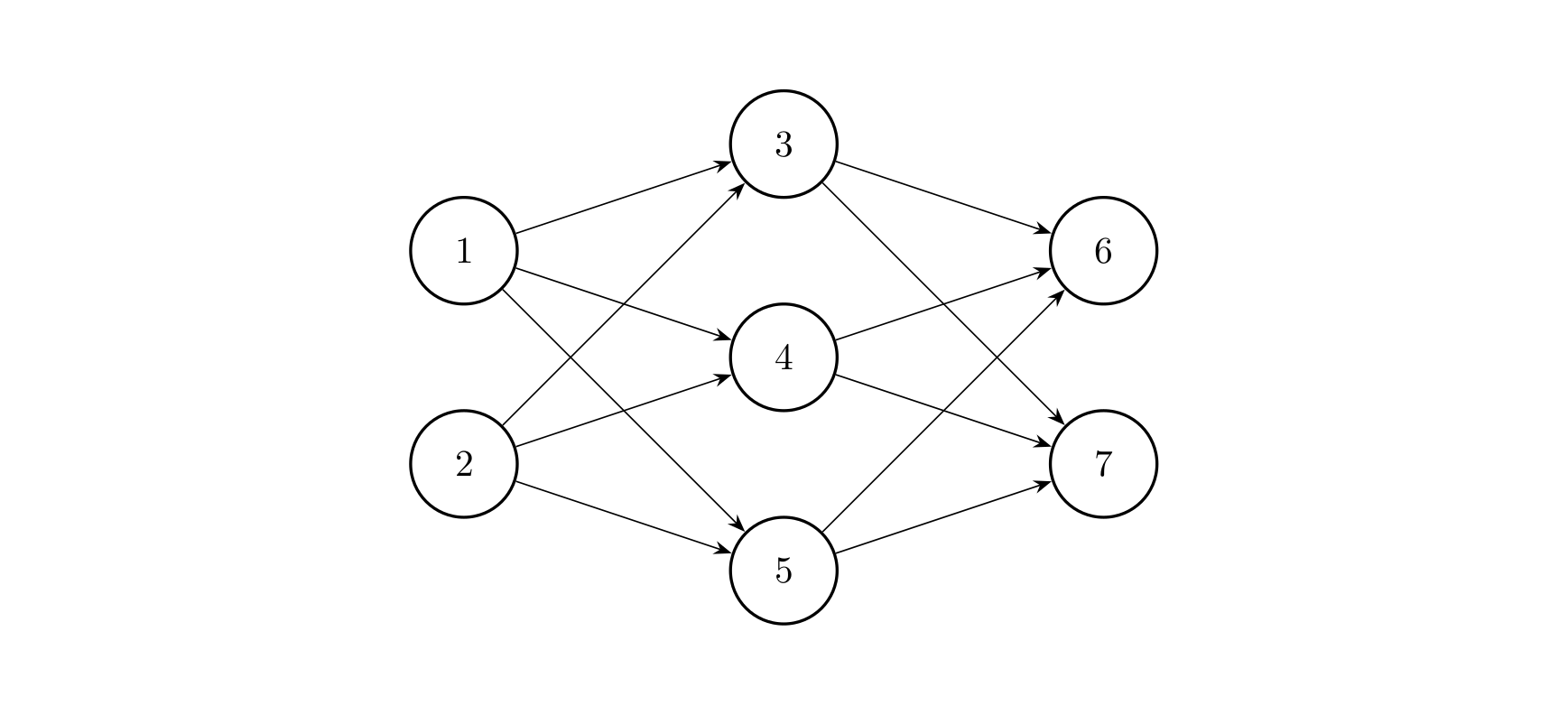Lanlan stipulates that $C_i$ follows the formula (where $n$ is the total number of neurons in the network): $$C_i=\left(\sum\limits_{(j,i) \in E} W_{ji}C_{j}\right)-U_{i}$$ Here, $W_{ji}$ (which may be negative) denotes the weight of the edge connecting neuron $j$ to neuron $i$. When $C_i$ is greater than $0$, the neuron is excited; otherwise, it is calm. When a neuron is excited, in the next second it will send signals to other neurons, with signal strength equal to $C_i$. Thus, after the neurons in the input layer are stimulated, the entire network operates under the push of information transmission. Now, given a neural network and the current states $C_i$ of the input-layer neurons, compute the final states of the output layer.

The first line contains two integers $n$ ($1 \le n \le 100$) and $p$. The next $n$ lines each contain $2$ integers; the $(i+1)$-th line gives neuron $i$’s initial state and its threshold $U_i$. Non–input-layer neurons start with state $0$. The following $p$ lines each contain three integers $i$, $j$, and $W_{ij}$ (where $W_{ij} \le 10^9$ and may be negative), indicating a directed edge from neuron $i$ to neuron $j$ with weight $W_{ij}$.

Output several lines, each containing $2$ integers: a neuron’s index and its final state, separated by a space. Output only those output-layer neurons whose final state is greater than $0$, in ascending order of index. If all output-layer neurons have final state less than or equal to $0$, output `NULL`.

[Problem Source] NOIP 2003 Senior, Problem 1. Translated by ChatGPT 5