P10393 无限循环？

你是一只小青蛙。 你被关进了塞拉飞舞监狱。 生活有点压抑，小青蛙幻想自己走出了塞拉飞舞监狱。 生活过于压抑，小青蛙开始反抗塞拉飞舞监狱。 小青蛙孤立无援，又被关进了塞拉飞舞监狱。 …… 循环不是无限的。如此往复，总有一天，他会将塞拉飞舞这黑暗的牢笼冲破！

小青蛙暂时被困在了循环里，这个循环可以看作一个有 $n$ 个点的环（$n$ 为奇数），每个点 $i$ 有点权 $a_i$。 对于所有的 $1 \leq i < n$，点 $i$ 和点 $i+1$ 之间有一条边，边权为 $w_i$；点 $1$ 和点 $n$ 之间有一条边，边权为 $w_n$。 这个环的边权和点权有奇妙的关系：对于任意一条边 $i$，其边权 $w_i$ 都必然满足关系 $w_i=\dfrac12(a_i+a_{i+1})$，其中 $w_n=\dfrac12(a_1+a_{n})$，当环中任意一条边的边权改变的时候，它的所有点点权会**随之改变**，直到所有点权都能与边权满足上述关系。 现在青蛙掌握了 $w_1\sim w_n$ 的值，而且他可以交换其中任意两条边的权值任意次（即任意打乱边权）。现在青蛙需要给出两组安排 $w_1\sim w_n$ 的方案，分别使得 $1$ 号点点权**在所有的排列方案中最大** / **最小**。 然而由于青蛙陷入了无限循环，他的脑子十分混乱，于是他向你寻求帮助，你需要帮他构造这样两组方案。 **题目保证 $\boldsymbol n$ 为奇数**。

无

无

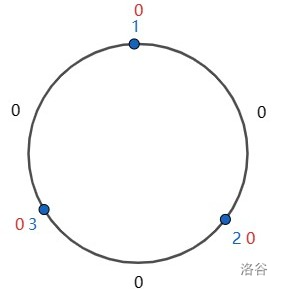
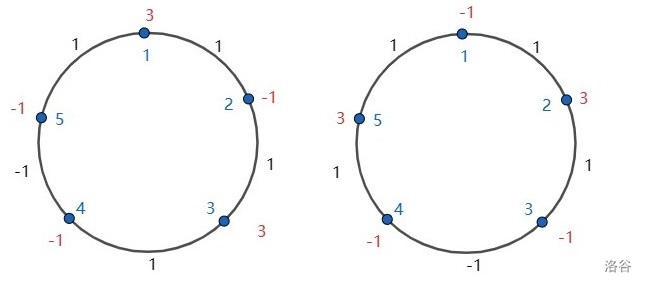
**【样例 #1 解释】**  其中红色数字表示点权，黑色数字表示边权，蓝色数字表示点的编号。 可以证明，这种方案下的 $1$ 号点权既最小，又最大。 **【样例 #2 解释】**  其中红色表示点权，黑色表示边权，蓝色表示点的号码。 可以证明，这两种方案下的 $1$ 号点权分别取到最大和最小。需要注意的是，这**不一定**是**唯一解**。 --- **【数据规模与约定】** **本题开启捆绑测试。** | $\text{Subtask}$ | 数据范围 | 分数 | 特殊性质 | | :----------: | :----------: | :----------: | :----------: | | $1$ | $n=3$ | $20$ | $\rm A$ | | $2$ | $n=3$ | $20$ | 无 | | $3$ | $n\leq 10^6$ | $20$ | $\rm B$ | | $4$ | $n\leq 10^6$ | $20$ | $\rm C$ | | $5$ | $n\leq 10^6$ | $20$ | 无 | - 特殊性质 $\rm A$ ：保证 $\{w\}$ 是由 $\{-1,0,1\}$ 任意打乱之后得到的一个序列。 - 特殊性质 $\rm B$ ：保证 $n \ge 3$，且对于所有 $i\in [2,n]$，有 $w_i$ 相同。 - 特殊性质 $\rm C$ ：保证 $n\ge 3$，且对于所有 $i\in [3,n]$，有 $w_i$ 相同。 - 对于 $100\%$ 的数据， $1\leq n\leq 10^6$ 且为奇数， $|w_i|\leq 10^9$。