P10395 青蛙寻青。

数次失败后，小青蛙的思想开始发生变化。 他开始寻找自己为青蛙之本。 他开始寻找其他青蛙帮忙。 他在发生蜕变。 他在升华。 他，将变成光！ 他给自己取了新名字 —— 青蛙青（qwq），因为名字很可爱。

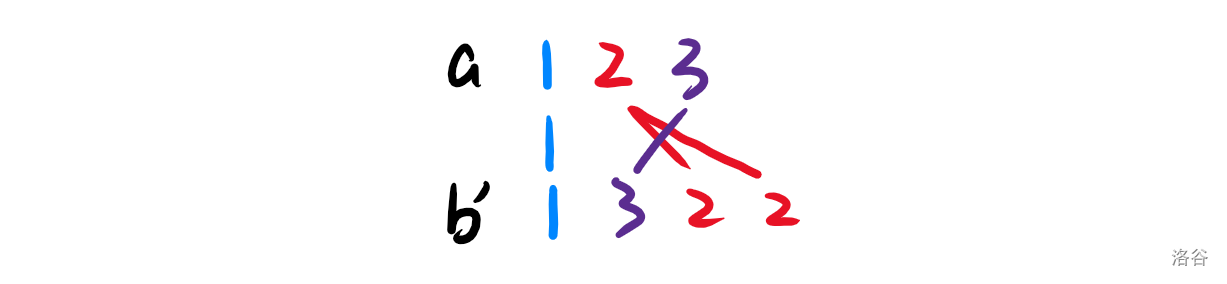
白色光可以被分解成青色光还有很多其他颜色的光。 $\{a\}$ 是一个长度为 $n$，有 $k$ 种不同颜色的序列，第 $i$ 个元素颜色为 $a_i$（保证颜色 $1\sim k$ 都在 $a$ 中出现过）。 $\{b\}$ 是一个长度为 $m$ 的序列，第 $i$ 个元素颜色为 $b_i$（保证每个 $b_i$ 都是 $k$ 种颜色中的一种，但不保证 $k$ 种颜色都在 $b$ 中出现过）。我们可以修改 $b$ 中若干个位置的颜色，得到一个长度仍为 $m$ 的序列 $b'$。 我们对 $b'$ 与 $a$ 中颜色相同的点连这种颜色的一条线段。 如 $n=3,m=4,k=3,a=\{1,2,3\},b'=\{1,3,2,2\}$，它们之间的连线是这样的：  要求**不同颜色的线段两两不交**，**且 $k$ 种颜色都要在 $b$ 中出现**，请问最少修改次数是多少？ 形式化的，设你修改后的符合要求的序列为 $b'$，那么你需要最小化： $$ \sum_{i=1}^{m}[b_i\ne b'_i] $$ 对于上述 $a=\{1,2,3\},b'=\{1,3,2,2\}$ 的情况，它们之间的连线（红色的 $2$ 与紫色 $3$ 之间）出现了相交。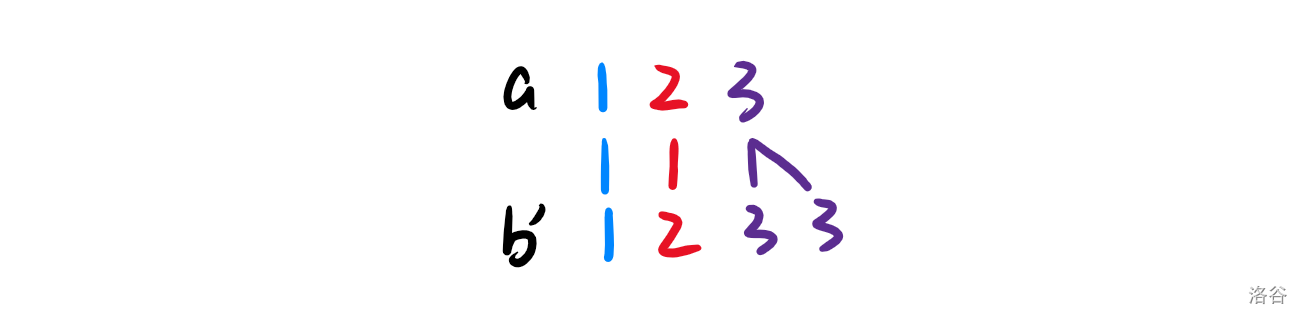 但如果我们把 $b$ 修改成 $\{1,2,3,3\}$，它们之间的连线没有相交，满足上述条件：  注意： - $b' = \{1,1,4,5\}$ 的情况连线也没有相交，但是 $b'$ 包含了 $k$ 种颜色之外的颜色（有 $4$ 和 $5$），因此这个 $b'$ 不合法。 - $b' = \{1,1,1,1\}$ 的情况连线也没有相交，但是 $b'$ 中没有包含 $1\sim k$ 中所有的颜色（没有 $2$ 和 $3$），因此这个 $b'$ 也不合法。 特别的，如果无论怎样修改都无法满足要求，请输出 `-1`。

无

无

**【样例 #1 解释】** 将 $\{1,3,2,2\}$ 修改为 $\{1,2,2,3\}$。 可以证明这是修改次数最少的方式。 **【样例 #2 解释】** 将 $\{1,2,3,3,3\}$ 修改为 $\{1,2,3,3,4\}$。 可以证明这是修改次数最少的方式。 --- **本题开启捆绑测试以及子任务依赖。** **本题时限 2s。** |$\text{Subtask}$| $n,m\le$ | 分数 | 子任务依赖 | |:---:|:---:|:---:|:---:| | $1$ | $5$ | $5$ | 无 | | $2$ | $5000$| $35$ | $1$ | | $3$ | $10^5$| $30$ | $1,2$ | | $4$ | $2\times 10^6$| $30$ | $1,2,3$ | - 对于 $100\%$ 的数据，保证 $1\le n,m\le 2\times 10^6$，$1\le a_i,b_i \le n$。设 $\max\limits_{i=1}^n{a_i} = k$，保证 $1\sim k$ 均在 $a$ 中出现过，且 $1\le k \le n$。