「QFOI R2」寺秋山霭苍苍

本题可能用到的公式： 两点间的距离公式：$(x_1,y_1),(x_2,y_2)$ 之间的距离为 $\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$。 海伦公式：若三角形三边长为 $a,b,c$，设半周长 $p=\frac{a+b+c}{2}$，则三角形面积为 $S=\sqrt{p(p-a)(p-b)(p-c)}$。

小 R 是一个可爱的女孩子，她的几何太差了，于是她向你求助这道几何题。 在平面直角坐标系中，有一个 $\triangle\textrm{ABC}$，其顶点坐标为 $\textrm{A}(x_1,y_1),\textrm{B}(x_2,y_2),\textrm{C}(x_3,y_3)$。 对于**实数** $p\in(0,1)$，在 $\textrm{BC},\textrm{CA},\textrm{AB}$ 边上分别取点 $\textrm{D},\textrm{E},\textrm{F}$，使得 $\frac{|\textrm{AF}|}{|\textrm{AB}|}=\frac{|\textrm{BD}|}{|\textrm{BC}|}=\frac{|\textrm{CE}|}{|\textrm{CA}|}=p$，则称 $\triangle\textrm{DEF}$ 为 $\triangle\textrm{ABC}$ 的“$p$ 比例三角形”。 请在 $[l,r]$ 范围内选择实数 $p$，使得 $\triangle\textrm{ABC}$ 的“$p$ 比例三角形”的面积最小。你需要求出这个面积。

一行八个**实数** $l,r,x_1,y_1,x_2,y_2,x_3,y_3$。

一行一个**实数** $S_{\min}$，表示最小面积。 你的输出被认为是正确的，当且仅当其与标准答案的绝对或相对误差不超过 $10^{-4}$。

0.40 0.60 0.00 0.00 4.00 0.00 1.00 5.00

2.500000000000

0.20 0.40 0.00 0.00 4.00 0.00 1.00 5.00

2.800000000000

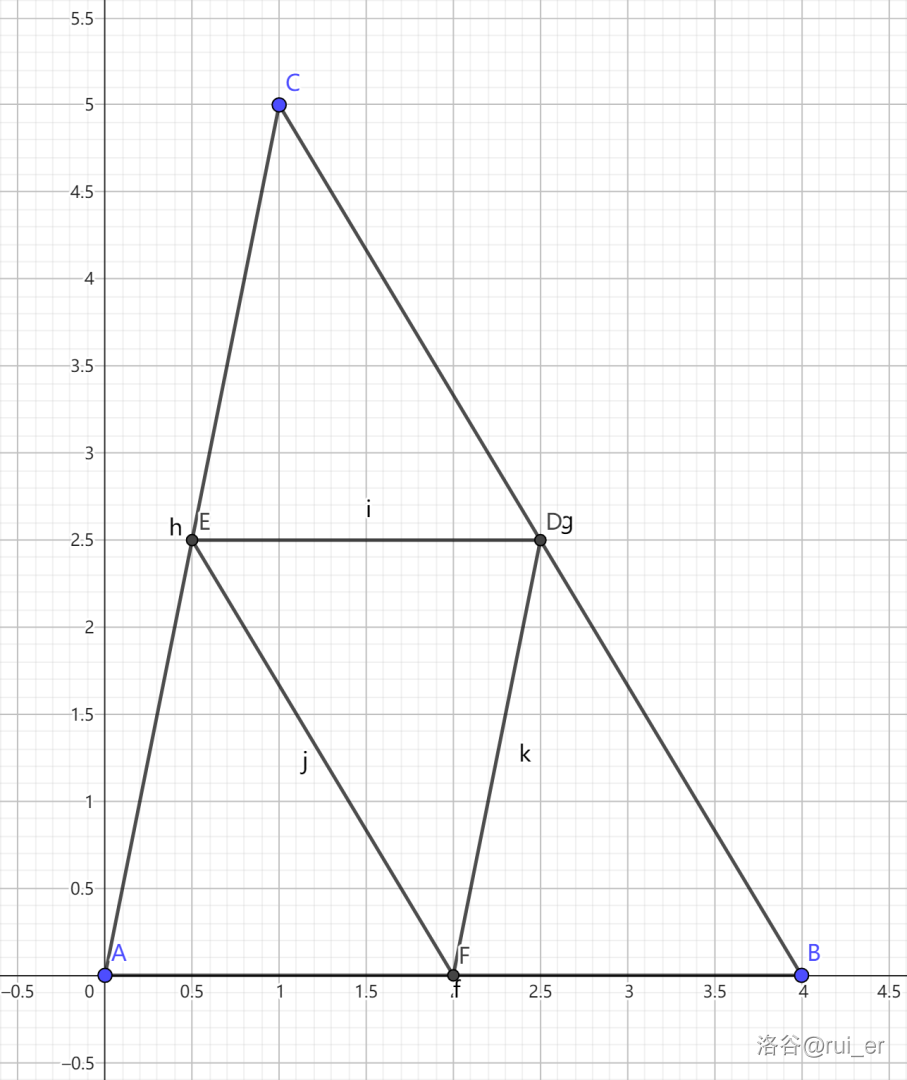
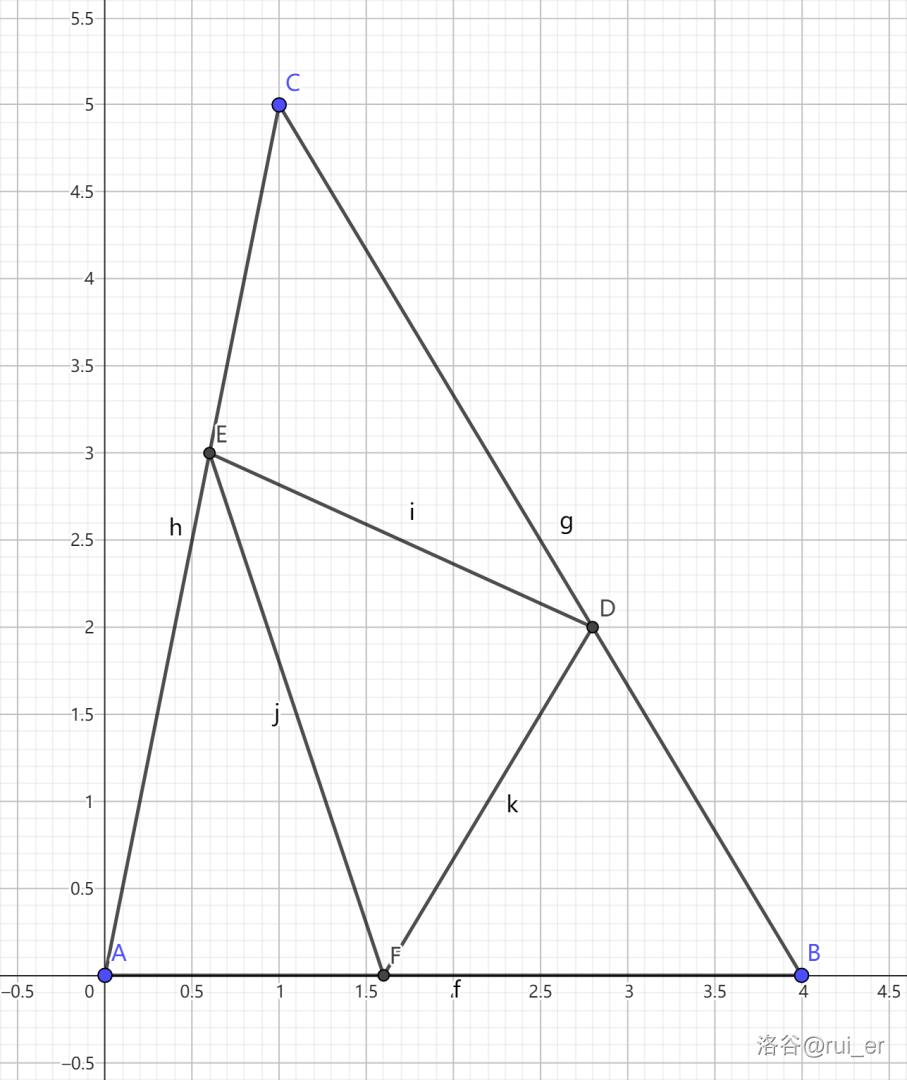
**样例 $1$ 解释** 可以证明，当 $p=0.5$ 时面积最小，为 $2.5$。  --- **样例 $2$ 解释** 可以证明，当 $p=0.4$ 时面积最小，为 $2.8$。  --- **评分方式** 本题采用自定义校验器（Special Judge）进行评测。 你的输出被认为是正确的，当且仅当其与标准答案的绝对或相对误差不超过 $10^{-4}$。 --- **数据范围** **本题采用捆绑测试。只有通过子任务中所有测试点以及所有依赖的子任务，才能获得相应的分数。** 对于全部数据：$0 < l < r < 1$，$0\le x_1,y_1,x_2,y_2,x_3,y_3\le 10^5$，保证输入构成三角形，所有实数的小数点后位数不超过 $2$。 - 子任务一（$20$ 分）：$l=0.10,r=0.90$。 - 子任务二（$20$ 分）：$x_1=y_1=y_2=x_3=0.00$。 - 子任务三（$20$ 分）：$x_1=y_1=y_2=0.00$。依赖子任务二。 - 子任务四（$40$ 分）：无特殊限制。依赖子任务一、二、三。 --- **提示** 本题可能用到的公式： 两点间的距离公式：$(x_1,y_1),(x_2,y_2)$ 之间的距离为 $\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$。 海伦公式：若三角形三边长为 $a,b,c$，设半周长 $p=\frac{a+b+c}{2}$，则三角形面积为 $S=\sqrt{p(p-a)(p-b)(p-c)}$。