P10605 Frustrating Paper

Renko has been struggling with inspiration for her paper. She has spent so much time on it that she hasn't had time to interact with her partner Merry.

One day, Renko discovered an excellent idea and wanted to refine it through experiments. Specifically, **she needs to complete $n$ tasks sequentially**, where the $i$-th task requires $a_i$ consecutive days to complete. This means if she starts the task on day $x$, she will finish it after day $x + a_i - 1$. She must ensure she is free on all those days. Unfortunately, she has $m$ days with prior commitments, given as a monotonically increasing sequence $b$. That is, for any $i$ ($1 \leq i < m$), $b_i < b_{i+1}$. Renko wants to minimize the total time taken to complete all tasks. For example: suppose she needs to complete 2 tasks, where the first takes 2 days and the second 3 days, and she has a commitment on day 4. 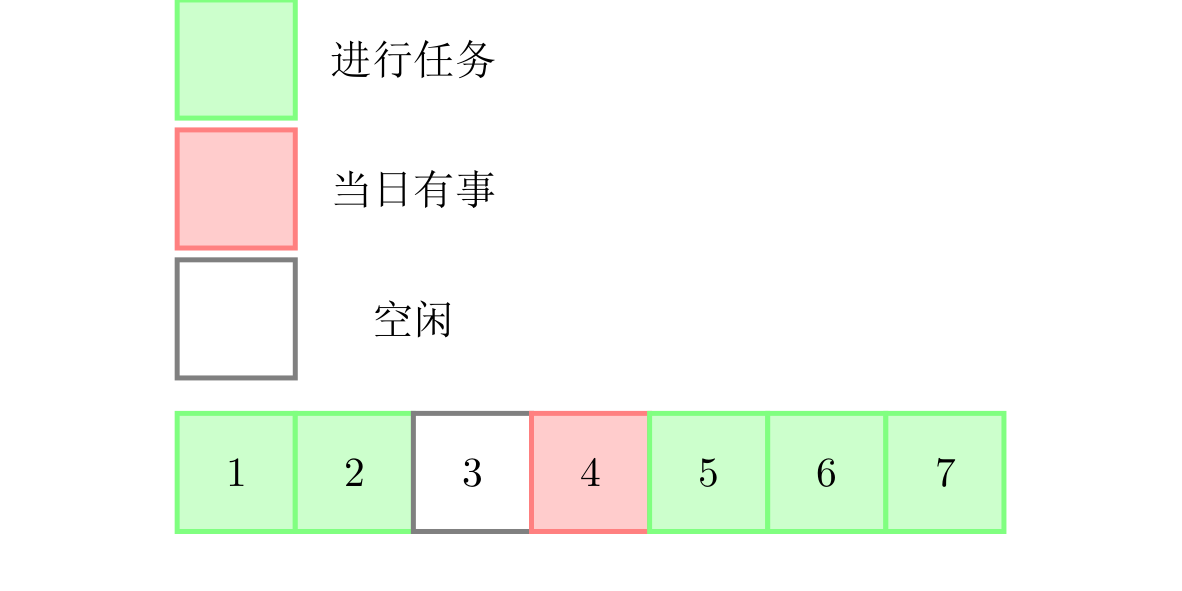The figure below shows a scenario where Renko finishes all tasks in the shortest possible time of 7 days:  - Green: be in progress - Red: be busy - Blank: spare time She wants to determine the earliest day she can complete all tasks under optimal conditions.

- The first line contains two integers $n$ and $m$. - The second line contains $n$ positive integers describing sequence $a$. - The third line contains $m$ positive integers describing sequence $b$, which is guaranteed to be monotonically increasing.

Output one integer: the earliest day Renko can finish all tasks.

### Sample #1 This matches the scenario described in the problem. Renko starts the first task on day 1 and finishes it after day 2. Due to her commitment on day 4, she cannot start the second task on day 3. Instead, she starts it on day 5 and completes it after day 7. This sample satisfies the special property of **Subtask 2**. ### Sample #2 Renko completes all tasks **consecutively** from day 2 to day 4. ### Constraints **Bundled testing is used. All test cases in a Subtask must be passed to receive its points.** Note: $\sum a_i$ denotes the sum of all $a_i$ (i.e., $a_1 + a_2 + \dots + a_n$). The same applies to other problems unless stated otherwise. $$ \def\arraystretch{1.5} \begin{array}{|c|c|c|c|c|c|c|}\hline \textbf{Subtask} & \textbf{Points} & \bm{n,m \leq} & \bm{\sum a_i \leq} & \bm{b_i \leq} & \textbf{Special Property} & \textbf{Subtask Dependencies} \cr\hline 1 & 20 & 10 & 100 & 100 & - & - \cr\hline 2 & 20 & 10^5 & 10^8 & 10^8 & m=1 & - \cr\hline 3 & 20 & 10^3 & 10^8 & 10^8 & \text{None} & - \cr\hline 4 & 40 & 10^5 & 10^8 & 10^8 & \text{None} & 1,2,3 \cr\hline \end{array} $$ For all data: $1 \leq n, m \leq 10^5$, $1 \leq a_i \leq \sum a_i \leq 10^8$, $1 \leq b_i \leq 10^8$, and $b$ is monotonically increasing. --- Translated by DeepSeek R1