P10606 Physics Experiment (Easy)

To refine her paper, Renko decides to study the physical properties of objects. Due to the overwhelming workload, she invites you to assist with a small experiment.

**This is the easy version of the problem. The difference between the two versions lies in the conditions the ball must satisfy. The full score for this version is 50 points.** Renko has a small ball initially at position $0$ on the number line and moving in the positive direction. She sets up devices at points $1$ to $n$ on the number line. When the ball passes through point $i$, she can pay a cost of $a_i$ to reverse its direction (from positive to negative, or vice versa). Renko has $m$ conditions to satisfy. The $i$-th condition states that "the ball must move from point $x_i$ to point $y_i$ at least once," **where** $x_i$ **is greater than** $y_i$. More precisely, this condition requires the ball's path to include a segment like $\ldots \to x_i \to \ldots \to y_i \to \ldots$. Renko wants to determine the minimum total cost required to satisfy all conditions.

- The first line contains two integers $n$ and $m$. - The second line contains $n$ positive integers describing the sequence $a$. - The next $m$ lines each contain two positive integers $x_i$ and $y_i$.

Output one integer: the minimum total cost required to satisfy all conditions.

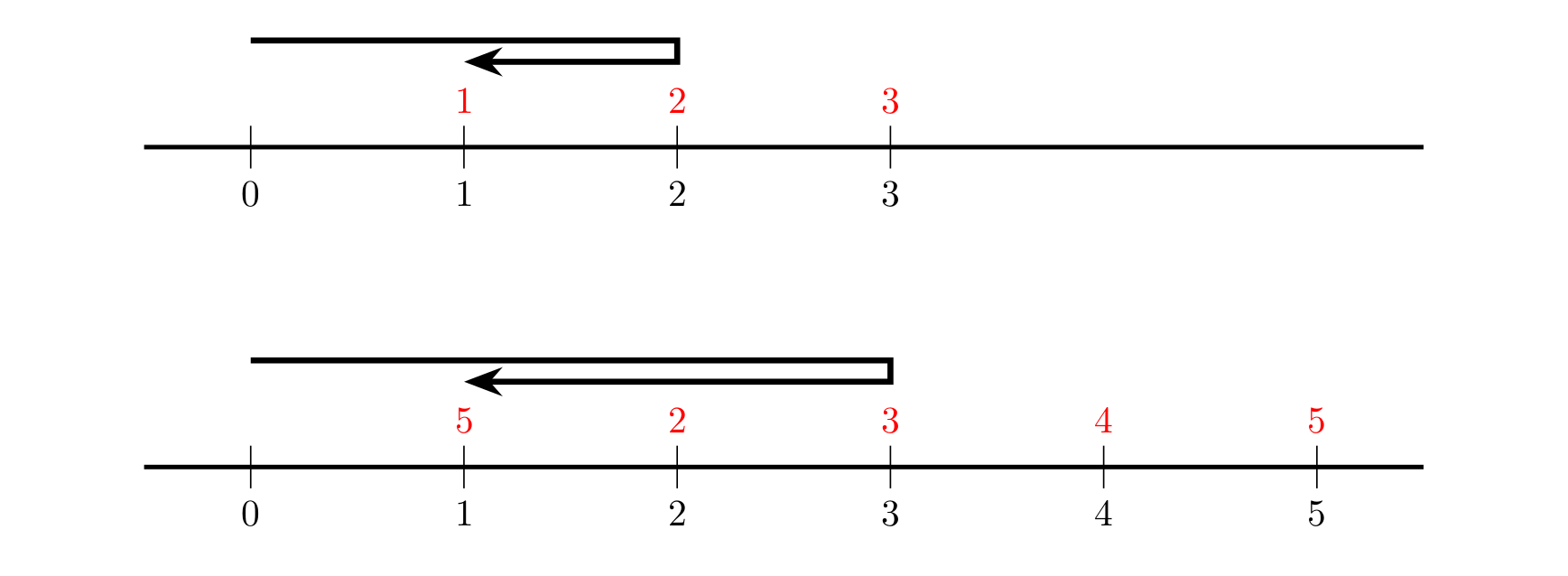
### Explanation  The figure above illustrates the movement paths for both samples. The numbers above the number line represent the reversal costs at each point, and the numbers below are coordinates. #### Sample #1 Renko reverses the ball's direction when it passes point $2$, satisfying all conditions with a total cost of $2$. #### Sample #2 Renko reverses the ball's direction when it passes point $3$, satisfying all conditions with a total cost of $3$. ### Constraints **Bundled testing is used.** $$ \def\arraystretch{1.5} \begin{array}{|c|c|c|c|c|c|c|}\hline \textbf{Subtask} & \textbf{Points} & \bm{n,m \leq} & \bm{a_i \leq} & \bm{x_i,y_i \leq} & \textbf{Special Property} & \textbf{Subtask Dependencies} \cr\hline 1 & 10 & 10 & 100 & 10 & - & - \cr\hline 2 & 10 & 10^3 & 10^8 & 10^3 & - & 1 \cr\hline 3 & 30 & 2 \times 10^5 & 10^8 & 2 \times 10^5 & - & 1,2 \cr\hline \end{array} $$ For all data: $1 \leq n, m \leq 2 \times 10^5$, $1 \leq a_i \leq 10^8$, $1 \leq y_i < x_i \leq n \leq 2 \times 10^5$. --- Translated by DeepSeek R1