P10623 [ICPC 2013 WF] Pirate Chest

海盗迪克终于厌倦了战斗、抢劫、偷窃，以及在开阔海域上给许多人带来的痛苦。因此，他决定退休，并找到了一个完美的岛屿，打算在那里度过余生，只要他不用尽光金币就行。他现在有大量的金币，想要把它们存放在一个箱子里（毕竟他是海盗）。迪克可以制造一个整数尺寸的矩形箱子，顶部尺寸的大小可以高达指定的最大尺寸，但高度可以是任意整数。现在他需要一个地方来隐藏这个箱子。在探索岛屿时，他找到了一个完美的解决方案。 迪克将把他的箱子藏在一个混浊的池塘中。池塘有一个矩形的表面，并完全填满了一个有高垂直岩壁的山谷底部。迪克调查了池塘，并了解到每个笛卡尔坐标网格系统方格的深度。当迪克将箱子浸入水中时，它将尽可能沉入，直到触及底部。箱子的顶部将保持与池塘表面平行，并且箱子将与网格方格对齐。被浸入水中的箱子所排开的水将抬高池塘表面的水平（即使周围没有空间供排开的水升起）。山谷的岩壁足够高，以至于水永远不会溅出山谷。当然，由于箱子必须看不见，它的顶部必须严格低于池塘表面。你的任务是找出海盗迪克能够用这种方式隐藏的最大箱子的容积。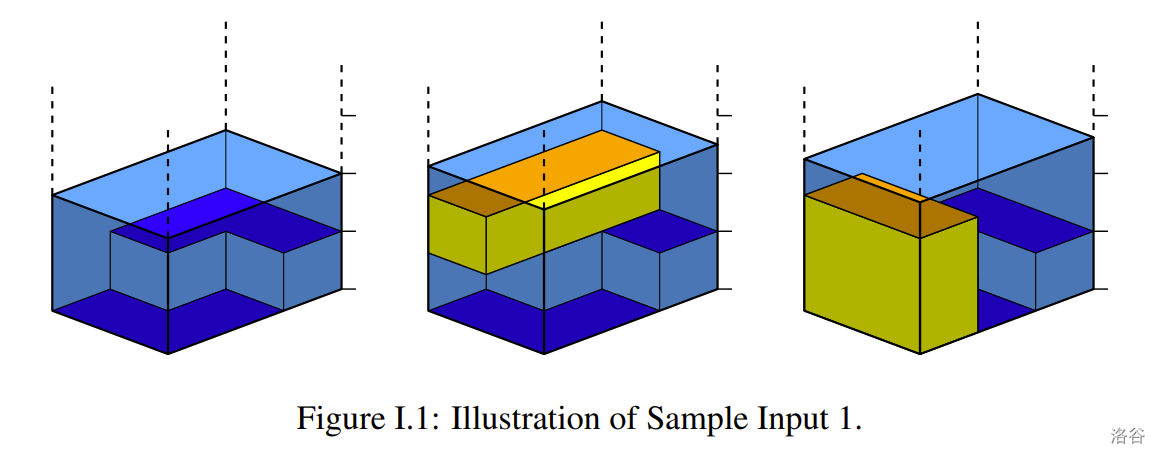 在图 I.1 中，最左边的图像显示了一个池塘，中间的图像显示了一个容积为 3 的箱子的可能摆放方式，最右边的图像显示了容积为 4 的箱子的摆放方式，这是可能的最大容积。请注意，如果第二个箱子的高度再增加一个单位，它的顶部将会可见，因为它的高度与水表面正好相同。 

输入包含一个测试用例。测试用例以一行四个整数 $a, b, m, n (1 \leq a, b, m, n \leq 500)$ 开始。池塘表面的尺寸为 $m \times n$，箱子顶部（和底部）的最大尺寸为 $a \times b$。此外，$a$ 和 $b$ 足够小，不能用顶部尺寸为 $a \times b$ 的箱子覆盖整个池塘。在测试用例的其余部分，每个深度的 $m$ 行中包含 $n$ 个整数 $d_{i,j}$，指定网格方格 $(i, j)$ 处的池塘深度，其中对于每个 $1 \leq i \leq m$ 和 $1 \leq j \leq n$，$0 \leq d_{i,j} \leq 10^9$。

显示能够完全浸入池塘表面以下的最大矩形箱子的容积。如果无法在池塘中隐藏箱子，则显示 $0$。 翻译来自于：[ChatGPT](https://chatgpt.com/)。