P10651 [ROI 2017] 虎（征集交互库） (Day 1)

### 题面 一个平面上有 $q$ 个信号发射器和 $n$ 个信号接收器，你知道每个信号接收器的位置，但是不知道信号发射器的位置。 你希望**依次**定位编号为 $1 \sim q$ 的信号发射器的位置，对于每个信号发射器，你可以使用不超过 $k$ 次如下方法通过信号接收器得到一些信息： - 选择 $m\ge 3$ 个接收器，系统会返回这 $m$ 个接收器顺次连接构建的凸包中是否有信号发射器。 当你得知了当前编号的信号发射器的位置时，你需要使用如下操作向交互库输出一种确定方案： - 选择 $m\ge 3$ 个接收器，这些接收器围成的凸包**内部**没有其他接收器，并且当前需要确认位置的发射器在凸包内部。 保证没有三个信号接收器位于同一直线，信号发射器不在穿过两个信号接收器的直线上，并且每个信号发射器都有至少一种合法的确定方案。 ### 交互过程 你可以编写一个函数 `findTiger()` 并在程序开始包含 `grader.h` 来完成交互过程。该函数无返回值，也没有参数。或者直接编写一个完整程序来进行交互。 你需要先从标准输出流中输入一个整数 $n$，表示信号接收器的个数。然后输入 $n$ 个坐标 $(x_i,y_i)$，表示接收器的位置。最后，你需要输入 $q$，即需要定位信号发射器的数量。 你可以向标准输出中输出询问和回答，形式如下： - 对于询问一个信号发射器是否在一个凸多边形内，你需要先输出一个字符 `?`，后跟一个整数 $m(3\le m\le n)$，表示查询的接收器数量，后跟 $m$ 个整数 $p_i(1\le p_i\le n)$，按逆时针顺序输出接收器的编号，字符，整数之间用一个空格隔开。如果当前信号发射器在查询的范围内，交互器会向标准输出中输出 $\texttt{Yes}$，否则会输出 $\texttt{No}$； - 对于回答一个信号接收器的位置，你需要先输出一个字符 `!`，后跟一个整数 $m(3\le m\le n)$，表示这个信号发射器在 $m$ 个接收器围成的凸多边形的范围内，后跟 $m$ 个整数 $p_i(1\le p_i\le n)$，按逆时针顺序输出接收器编号，要求围成的范围内没有接收器且有当前的信号发射器。字符，整数之间用一个空格隔开。 你需要按顺序寻找每个信号接收器的位置。保证信号接收器的位置在交互过程中不会改变，如果有多个凸多边形可以确定信号接收器的位置，你可以回答任意一个。

无

无

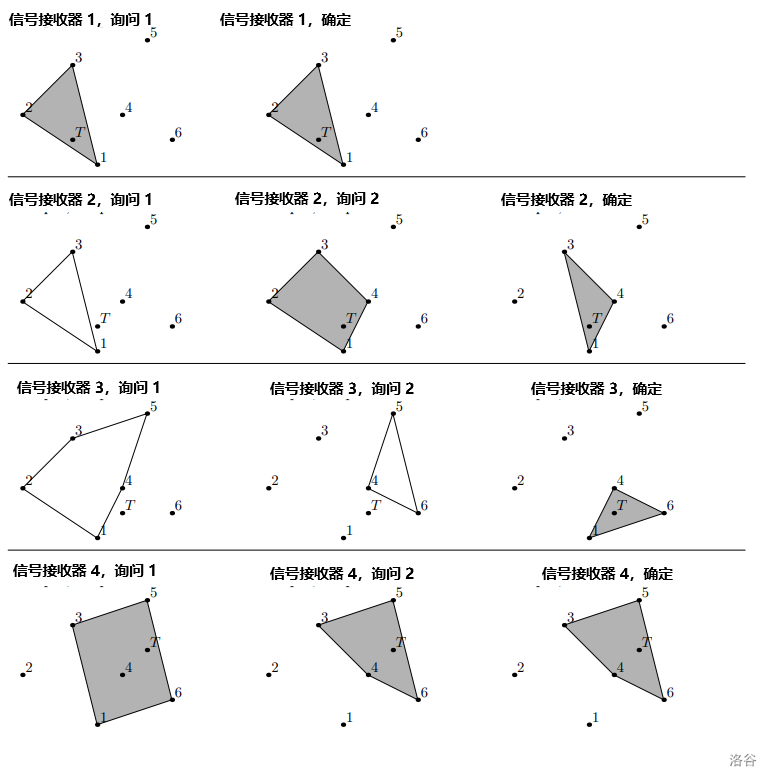
#### 【提示】 下面展示了一种交互的过程：  #### 【数据范围】 注：本题缺少交互库，完整数据请左转 [LOJ P2768](https://loj.ac/p/2768) 评测。 |子任务编号|分值|$3 \le n \le$|$1 \le q \le $|$k=$| |:-----------:|:-----------:|:-----------:|:-----------:|:-----------:| |$1$|$15$|$6$|$50$|$4000$| |$2$|$17$|$20$|$50$|$4000$| |$3$|$9$|$60$|$400$|$4000$| |$4$|$9$|$300$|$1000$|$600$| |$5$|$10$|$5000$|$10$|$10000$| |$6$|$10$|$300$|$1000$|$250$| |$7$|$10$|$1000$|$1000$|$200$| |$8$|$10$|$1000$|$2000$|$60$| |$9$|$10$|$2500$|$2000$|$40$|