P10657 BZOJ4998 星球联盟

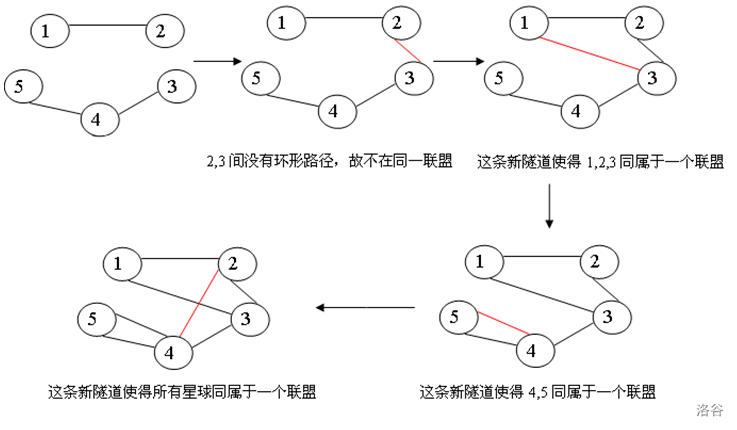
在遥远的 S 星系中一共有 $n$ 个星球，编号为 $1\sim n$。其中的一些星球决定组成联盟，以方便相互间的交流。但是，组成联盟的首要条件就是交通条件。 初始时，在这 $n$ 个星球间有 $m$ 条太空隧道。每条太空隧道连接两个星球，使得它们能够相互到达。若两个星球属于同一个联盟，则必须存在一条环形线路经过这两个星球，即两个星球间存在两条没有公共隧道的路径。为了壮大联盟的队伍，这些星球将建设 $p$ 条新的太空隧道。这 $p$ 条新隧道将按顺序依次建成。一条新轨道建成后，可能会使一些星球属于同一个联盟。 你的任务是计算出，在一条新隧道建设完毕后，判断这条新轨道连接的两个星球是否属于同一个联盟，如果属于同一个联盟就计算出这个联盟中有多少个星球。

第一行三个整数 $n,m,p$，分别表示总星球数，初始时太空隧道的数目和即将建设的轨道数目。 第 $2\sim m+1$ 行，每行两个整数，表示初始时的每条太空隧道连接的两个星球编号。 第 $m+2$ 行到第 $m+p+1$ 行，每行两个整数，表示新建的太空隧道连接的两个星球编号。 这些太空隧道按照输入的顺序依次建成。

输出共 $p$ 行： - 如果这条新的太空隧道连接的两个星球属于同一个联盟，就输出一个整数，表示这两个星球所在联盟的星球数。 - 如果这条新的太空隧道连接的两个星球不属于同一个联盟，就输出 No。

 数据保证，$1\leq n,m,p \leq 2\times 10^5$。