『STA - R6』月


对于一棵有 $n$ 个节点的树 $T$，定义其直径 $\operatorname{diam}(T)$ 为任意两个节点之间距离的最大值。 给定正整数 $n$ 和每个点 $i$ 的度数 $d_i$，你需要构造一棵树 $T^\prime$，同时最小化 $\operatorname{diam}(T^\prime)$。 保证至少存在一棵符合要求的树，若存在多个符合要求的答案，输出任意一个即可。

**本题单个测试点内含有多组测试数据。** 第一行一个正整数 $T$，代表测试数据组数。 对于每组测试数据， - 第一行一个正整数 $n$。 - 第二行 $n$ 个正整数，第 $i$ 个正整数表示点 $i$ 的度数 $d_i$。

对于每组测试数据，输出 $n - 1$ 行，每行两个正整数 $u_i, v_i$，表示构造出的树的边集。

4
2
1 1
3
1 1 2
5
1 1 2 2 2
7
1 3 2 3 1 1 1

2 1
1 3
3 2
5 4
4 2
3 1
3 5
4 2
3 2
1 2
5 4
6 4
7 3

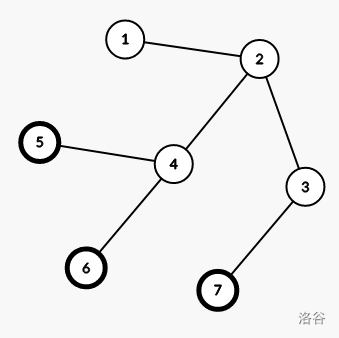
**【样例解释】** 对于最后一组数据，所构造出的树如下图：  其直径等于点 $5,7$ 之间或点 $6,7$ 之间的距离，为 $4$。可以证明，不存在满足条件的直径小于 $4$ 的树。 **【数据范围】** **本题采用捆绑测试。** 对于 $100\%$ 的数据： - $2 \le n \le 2 \times 10^5$； - $1 \le T \le 10^5$； - $\sum n \le 2 \times 10^5$； - $1 \le d_i < n$； - 保证至少存在一个合法的解。 具体部分分分配如下： |Subtask 编号|数据范围|分值| |:--------:|:--------:|:--------:| |1|$n \le 5$|$17$| |2|$d_i \le 2$|$23$| |3|$d$ 中只含有两种本质不同的元素|$26$| |4|无特殊限制|$34$|