P10678 『STA - R6』Moon


For a tree $T$ with $n$ nodes, its diameter $\operatorname{diam}(T)$ is defined as the maximum distance between any two nodes. Given a positive integer $n$ and the degree $d_i$ of each node $i$, construct a tree $T^\prime$ that minimizes $\operatorname{diam}(T^\prime)$. It is guaranteed that at least one valid tree exists. If multiple valid answers exist, output any one of them.

**This problem contains multiple test cases within a single test point.** The first line contains a positive integer $T$, representing the number of test cases. For each test case: - The first line contains a positive integer $n$. - The second line contains $n$ positive integers, where the $i$-th integer denotes the degree $d_i$ of node $i$.

For each test case, output $n - 1$ lines. Each line contains two positive integers $u_i$ and $v_i$, representing the edges of the constructed tree.

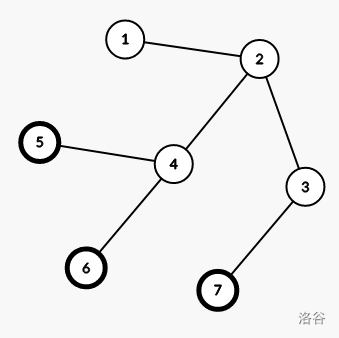
**Sample Explanation** For the last test case in the sample input, the constructed tree is shown below:  Its diameter equals the distance between nodes $5$ and $7$ or nodes $6$ and $7$, which is $4$. It can be proven that no tree satisfying the conditions has a diameter smaller than $4$. **Data Constraints** **This problem uses subtask scoring.** For $100\%$ of the data: - $2 \le n \le 2 \times 10^5$; - $1 \le T \le 10^5$; - $\sum n \le 2 \times 10^5$; - $1 \le d_i < n$; - It is guaranteed that at least one valid solution exists. Detailed subtask allocations are as follows: | Subtask ID | Data Range | Points | |:----------:|:----------:|:------:| | 1 | $n \le 5$ | 17 | | 2 | $d_i \le 2$| 23 | | 3 | $d$ contains only two distinct values | 26 | | 4 | No additional constraints | 34 | Translation by DeepSeek R1