[SNCPC2024] 最大流

给定一个 $n$ 个点 $m$ 条边的有向无环图，图中每条边的容量为 $1$。对点 $1$ 以外的每个点 $i$，设从点 $1$ 到点 $i$ 的最大流为 $f_i$，试求出 $\min\{f_i,\ k\}$。 在边容量为 $1$ 的图上，一个从点 $1$ 到点 $i$ 的流即为一条从点 $1$ 到点 $i$ 的路径。如果从点 $1$ 到点 $i$ 最多能同时有 $f_i$ 个不交的流（即没有一条边同时属于两个流），则我们认为点 $1$ 到点 $i$ 的最大流是 $f_i$。

输入第一行为三个整数 $n, m, k$ ($2 \leq n \leq 10^5, 1 \leq m \leq 2 \times 10^5, 1 \leq k \leq 50$)，由空格隔开，为图的点数，边数和参数。 接下来 $m$ 行，每行两个整数 $x_i,y_i$ ($1 \leq x_i, y_i \leq n, x_i \neq y_i$)，由空格隔开，描述一条有向边。 图中保证没有自环，但是可能存在重边，保证给出的是一个有向无环图。

输出仅一行 $n-1$ 个整数，由空格隔开。对于第 $i$ 个整数，如果从结点 $1$ 到结点 $i+1$ 的最大流不超过 $k$，则为最大流的值，否则为 $k$。

7 12 3
1 2
1 3
3 2
3 4
2 4
1 5
5 6
3 6
1 7
5 7
6 7
4 7

2 1 2 1 2 3 

5 8 50
1 2
1 2
1 2
3 2
2 4
2 4
2 4
2 4

3 0 3 0 

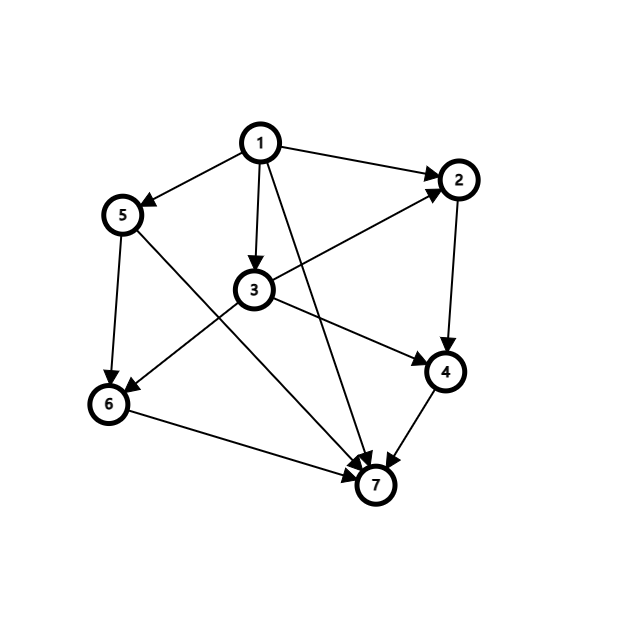
第一个样例所述图如下：  我们可以找到 $4$ 条从点 $1$ 到点 $7$ 的不相交路径： $\text{1->7}$ $\text{1->5->7}$ $\text{1->3->6->7}$ $\text{1->2->4->7}$ 我们无法找到更多条从点 $1$ 到点 $7$ 的不相交路径： 所以点 $1$ 到点 $7$ 的最大流为 $f_7=4$，但是因为 $k=3$，所以答案的第六个整数为 $3$。