P10703 [SNCPC2024] 窗花

有一扇 $100 \text{cm} \times 100 \text{cm}$ 的窗户和 $n$ 个对角线长为 $2 \text{cm}$ 的正方形窗花。建立坐标系，以窗户左下角的坐标为原点 $(0,0)$，右上角坐标为 $(100,100)$，第 $i$ 个窗花中心被贴在非边缘的整坐标点 $(x_i,y_i)$ ($1 \leq x_i,y_i \leq 99$) 上，窗花的对角线与坐标轴平行。 问窗户有多大的面积被至少一片窗花覆盖。

第一行一个整数 $n$ ($1 \leq n \leq 10000$)。 接下来 $n$ 行，每行两个整数 $x_i,y_i$ ($1 \leq x_i,y_i \leq 99$)，含义如上所述。

输出仅一行一个实数，为被至少一片窗花覆盖的面积。 你的答案被认为正确当且仅当其相对误差或绝对误差不超过 $10^{−4}$。形式化地说，假设你的答案是 $a$，标准答案是 $b$。你的答案被认为正确当且仅当 $\frac{|a−b|}{\max (1,|b|)} \leq 10^{−4}$。

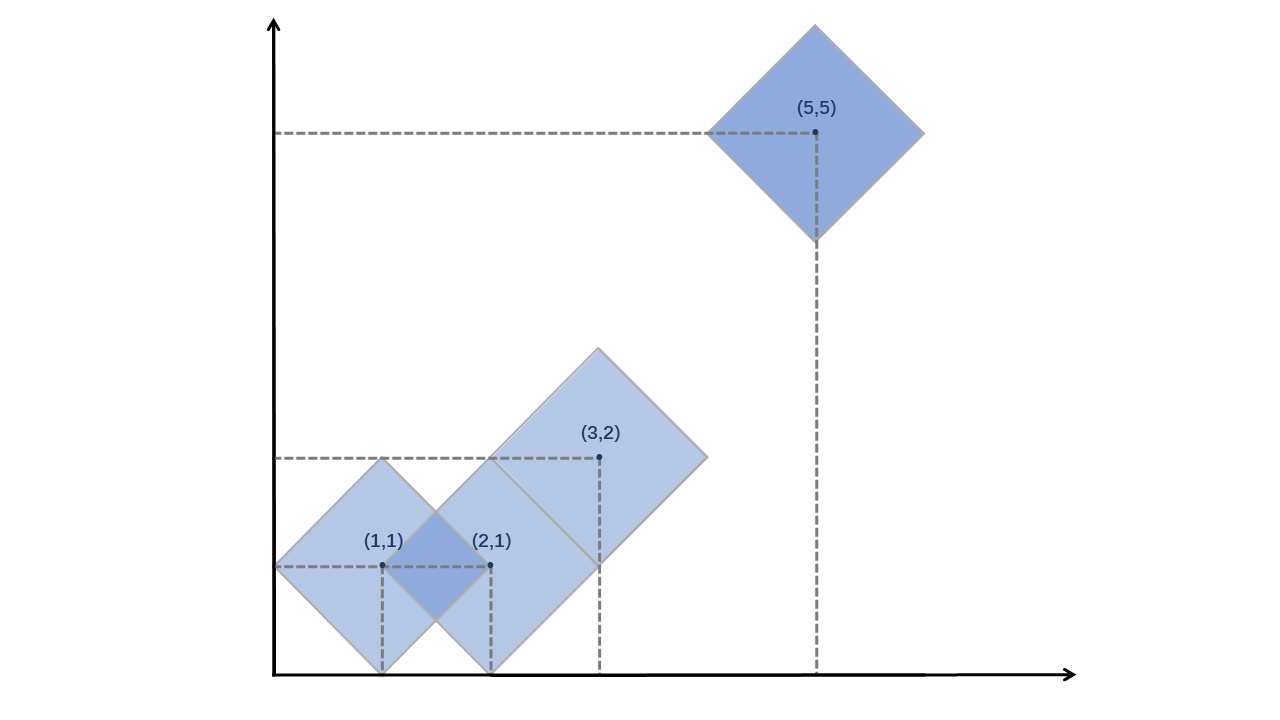
对于第一个样例的解释如图：