P10718 【MX-X1-T6】「KDOI-05」简单的图上问题

原题链接：。

给你一个 $n$ 个点 $m$ 条边的边双连通图，并且给定了每个点的坐标，保证每条边不相交或者只在端点处重合。 给定 $k$ 个图上的简单环 $C_1,C_2,\dots,C_k$，定义 $G_i$ 为只考虑 $C_i$ 内部的点和边所组成的图。 对 $S\subseteq\{1,2,\dots,k\},S=\{s_1,s_2,\dots,s_t\}$，定义 $f(S)$ 表示所有 $G_{s_i}$ 交的连通块数量。 有 $q$ 个询问，每次给出一个 $z$，输出 $\sum_{S\subseteq\{1,2,\dots,k\},|S|=z}f(S)$。对 $998244353$ 取模。

第一行三个正整数表示 $n,m,k$。 接下来 $n$ 行，每行两个整数 $(x_i,y_i)$ 表示第 $i$ 个点的坐标。保证所有 $1\leq i

输出 $q$ 行，每行一个整数表示 $\sum_{S\subseteq\{1,2,\dots,k\},|S|=z}f(S)$ 对 $998244353$ 取模后的值。

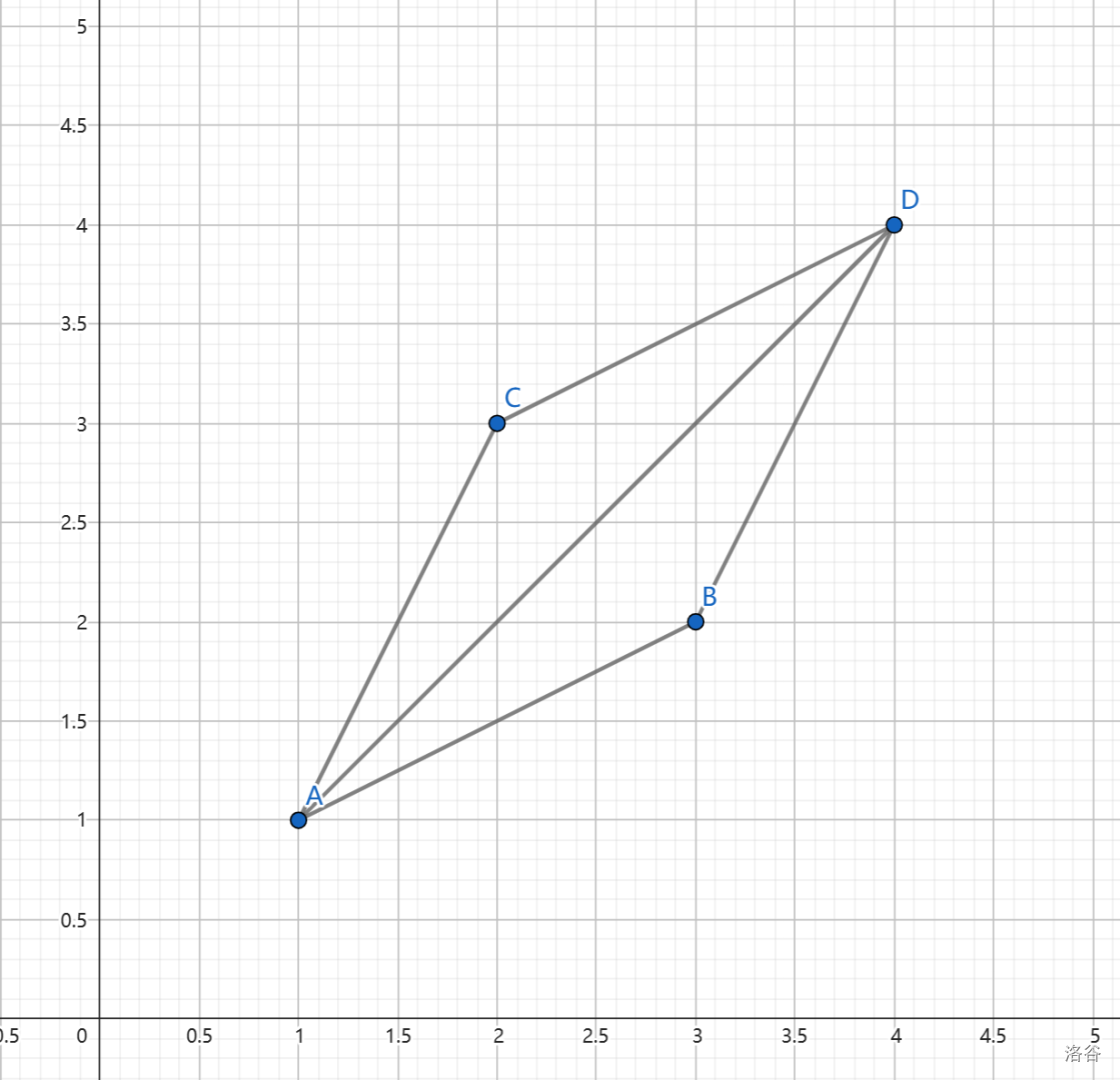
**【样例解释 \#1】** 样例 $1$ 的数据如图：  **【数据范围】** **本题采用捆绑测试。** | 子任务编号 | 分值 | $n\leq$ | 特殊性质 | |:--:|:--:|:--:|:--:| | $1$ | $15$ | $10$ | 无 | | $2$ | $30$ | $1000$ | 无 | | $3$ | $30$ | $4\times10^4$ | 保证平面图是一个凸包的三角剖分 | | $4$ | $15$ | $4\times10^4$ | 无 | | $5$ | $10$ | $10^5$ | 无 | 对于 $100\%$ 的数据：$1\leq n,\sum l_i\leq10^5$，$1\leq m\leq 3n-6$，$3\leq l_i$，$0\leq |x_i|,|y_i|\leq 10^9$，$1\leq q\leq 20$，$1\leq u_i,v_i\leq n$，$u_i\neq v_i$，$1\leq z_i\leq k$。保证所有 $1\leq i