P1074 [NOIP 2009 Senior] Target Sudoku

**此为远古题，不保证存在可以通过任意符合要求的输入数据的程序**。

Xiaocheng and Xiaohua are both good students who love mathematics. Recently, they have both become fascinated with Sudoku. Competitive as they are, they want to use Sudoku to compete. However, ordinary Sudoku is too easy for them, so they consulted Dr. Z, who brought out his recently invented “Target Sudoku” as their challenge. The grid of Target Sudoku is the same as ordinary Sudoku: in a $9 \times 9$ large grid there are $9$ small $3 \times 3$ subgrids (separated by bold black lines). In this large grid, some numbers are already given. Based on these numbers, use logical reasoning to fill the empty cells with digits $1$ to $9$. Each digit cannot repeat within any small $3 \times 3$ subgrid, and cannot repeat within any row or column. Target Sudoku differs from ordinary Sudoku in one respect: each cell has a score, and like a target, the closer it is to the center, the higher the score (see figure).  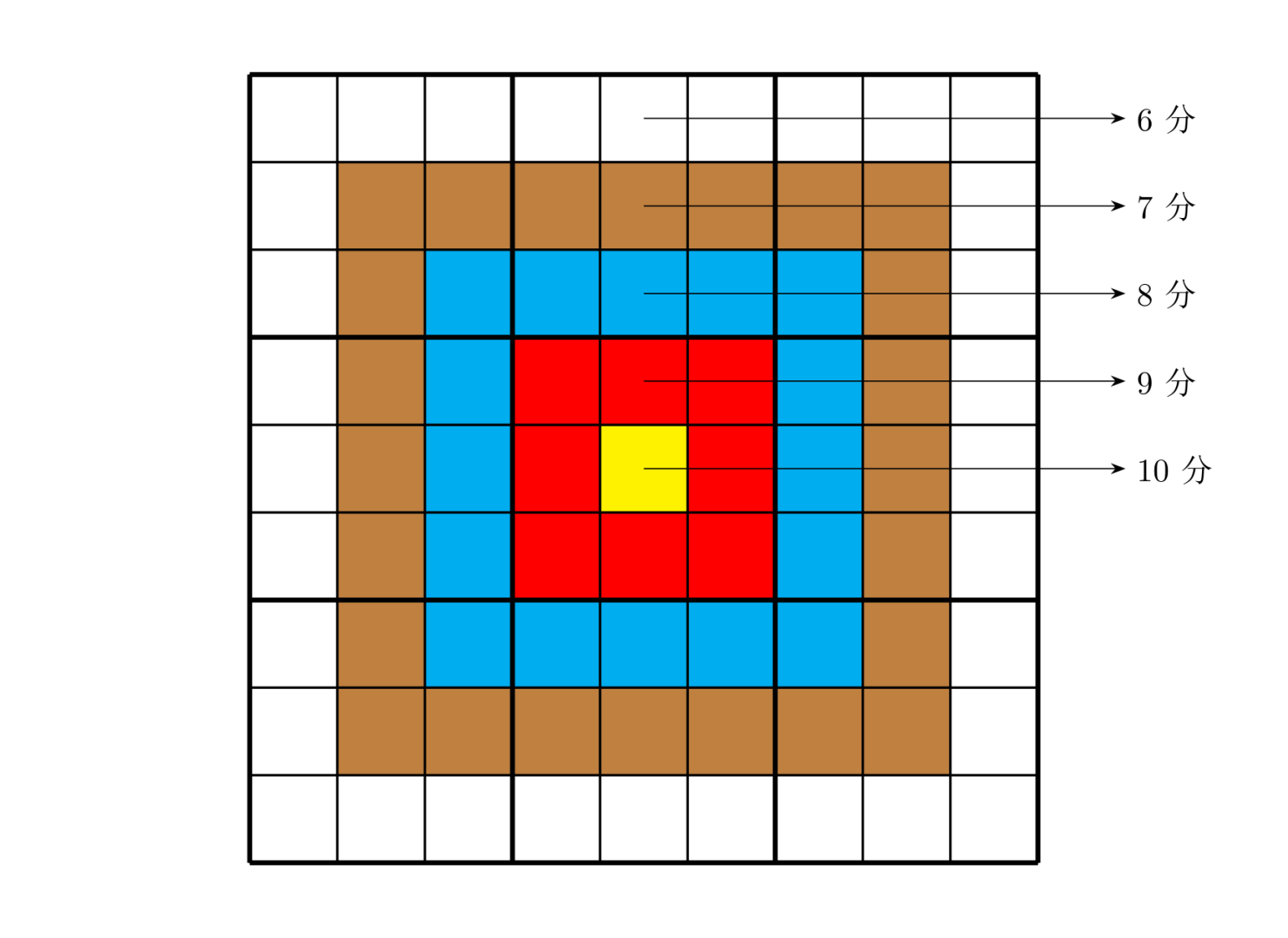The specific score distribution is: the innermost single cell (yellow region) is worth $10$ points; the ring outside the yellow region (red region) is $9$ points per cell; the next ring (blue region) is $8$ points per cell; the ring outside the blue region (brown region) is $7$ points per cell; and the outermost ring (white region) is $6$ points per cell, as shown above. The task is: each person must complete a given Sudoku (each given Sudoku may have multiple valid completions), and strive for the highest total score. The total score is the sum, over all cells, of the product of the cell’s score and the digit filled in that cell when the Sudoku is completed. 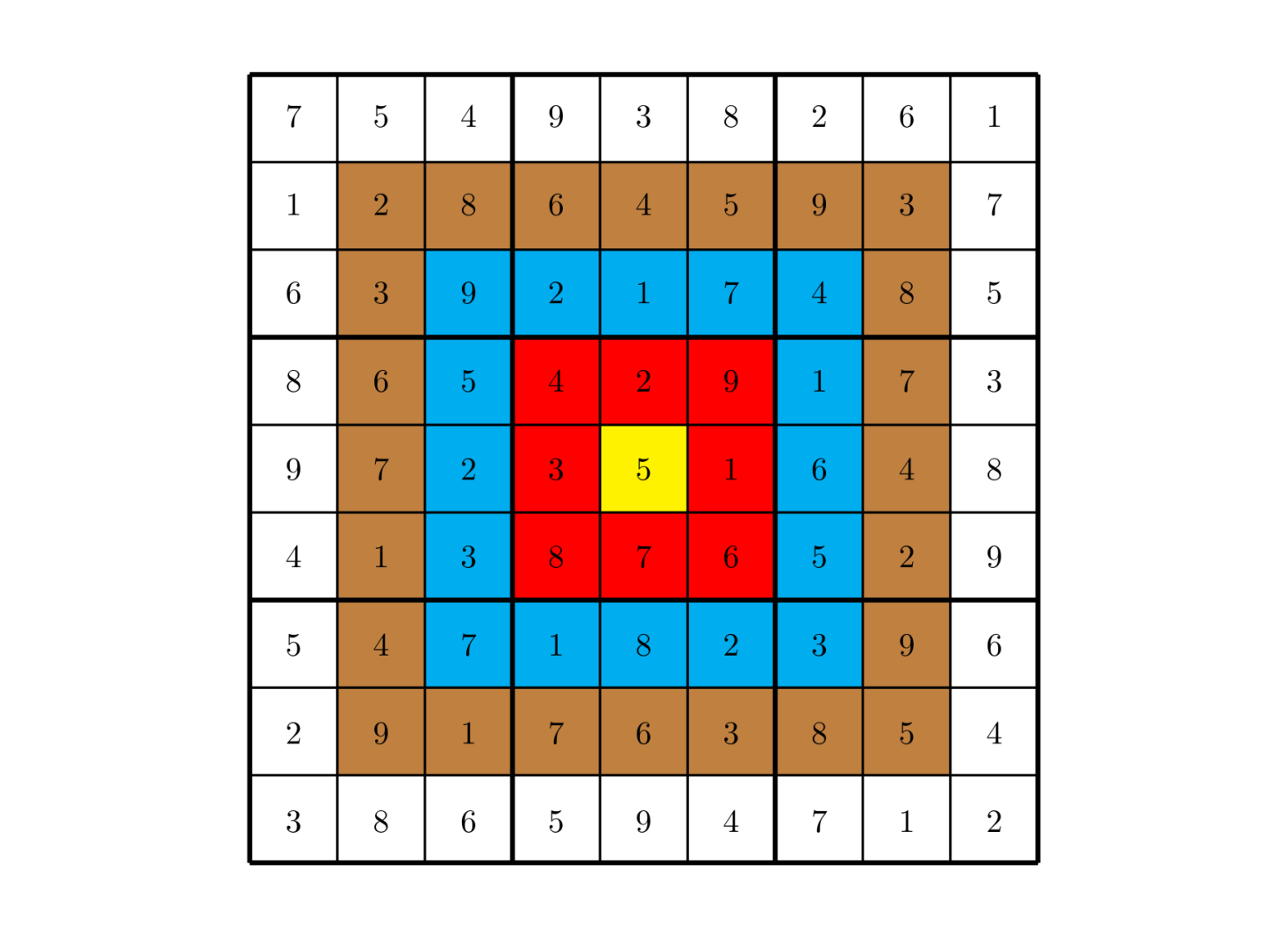As shown below, in this completed Target Sudoku, the total score is $2829$. The game rules determine the winner by comparing total scores.  Eager to win, Xiaocheng turns to you, a skilled programmer, to compute the highest possible total score for a given Target Sudoku.

There are $9$ lines in total. Each line contains $9$ integers (each between $0$ and $9$ inclusive), representing a partially filled Sudoku grid. Unfilled cells are represented by $0$. Each pair of integers is separated by a single space.

Output a single line: the maximum total score achievable for the given Target Sudoku. If the Sudoku has no solution, output $-1$.

- Constraints: - For $40\%$ of the testdata, the number of non-zero entries in the Sudoku is at least $30$. - For $80\%$ of the testdata, the number of non-zero entries in the Sudoku is at least $26$. - For $100\%$ of the testdata, the number of non-zero entries in the Sudoku is at least $24$. NOIP 2009 Senior, Problem 3. Translated by ChatGPT 5