P10754 [COI 2023] Nestabilnost

题目来源：。

河对岸的松林，一小时前还沐浴在五月的阳光下，此刻却变得模糊、朦胧、消散。只剩下一棵巨大的树，一棵有 $N$ 个节点的树…… 伊万在 119 号房间里，观察着这棵牢牢扎根于编号为 1 的节点的树。在更仔细地观察了这棵树之后，他注意到每个节点 $i$ 上都有一个数字 $a_i$。突然，一个 **$k$-好子树** (k-dobrog podstabla) 的定义闪现在他的脑海中。如果对于一个子树中的每一条连接节点 $(u, v)$（其中 $u$ 是 $v$ 的父节点）的边，都满足 $a_v = (a_u + 1) \pmod k$，并且对于该子树内的每个节点 $v$，都满足 $a_v < k$，那么这个子树就是 **$k$-好的**。对于每个数字 $k$，存在一个 **$k$-好**子树的自然不稳定性，记为 $f(k)$。 当他再次回过神来，他注意到树前漂浮着一个木筏，而他的右手里握着一把魔法锯子。伊万决定锯掉一些树枝（边），对于通过移除被锯掉的边而得到的每个连通块（子树），他都会选择一个数字 $k_i$，使得该连通块是 **$k_i$-好的**。伊万决定将这样的一组选择——即选择一组要切断的边，并为每个因此得到的子树选择一个满足条件的 $k_i$（使得该子树是 **$k_i$-好的**）——称为一次 **切割 (rezanjem)**。一次 **切割** 的 **不稳定性 (Nestabilnost)** 定义为所有得到的子树的 $f(k_i)$ 之和。请帮助伊万确定一次 **切割** 可能的最小 **不稳定性**！

第一行是一个正整数 $N$，表示树的节点数。 第二行是 $N$ 个整数，第 $i$ 个数表示 $a_i$ ($0 \le a_i \le N - 1$) 。 第三行是 $N$ 个整数，第 $k$ 个数表示 $f(k)$ ($1 \le f(k) \le 10^9$) 。 接下来的 $N-1$ 行描述了这棵树的结构，第 $i$ 行包含两个整数 $u_i$ 和 $v_i$ ($1 \le u_i, v_i \le N, u_i \ne v_i$)，表示节点 $u_i$ 和 $v_i$ 之间有一条边。

在唯一的一行中，输出一次 **切割** 可能的最小 **不稳定性**。

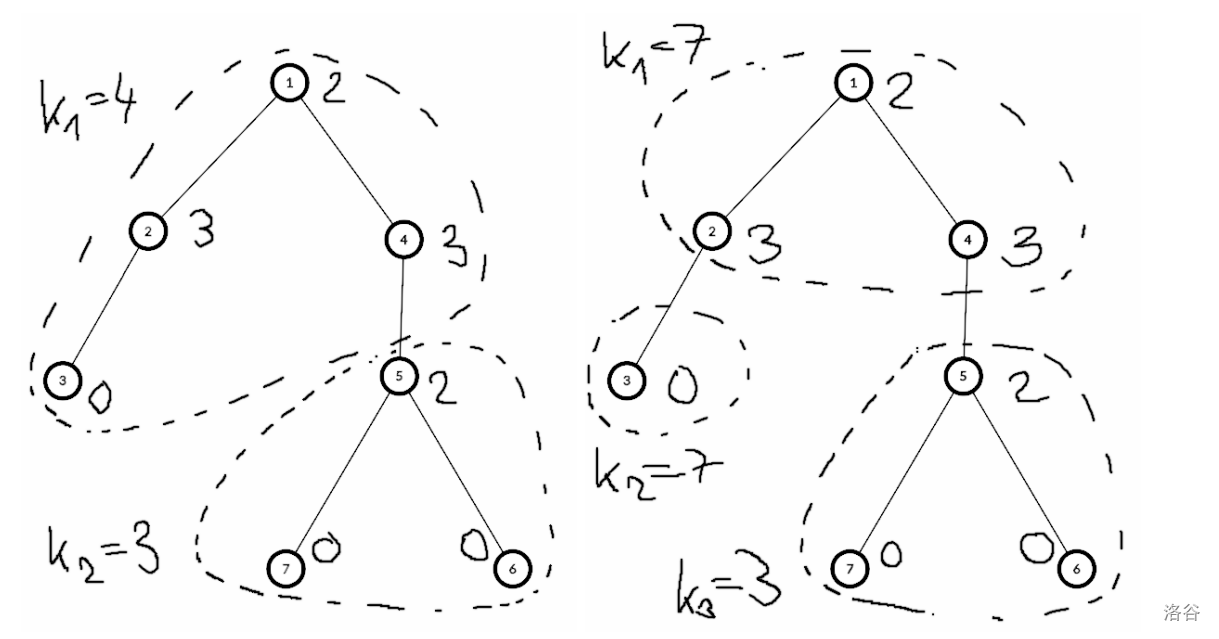
**【样例解释】**  左图为样例 1，右图为样例 2。 **【数据范围】** 在所有子任务中，都满足 $1 ≤ N ≤ 3\times 10^5$ 的条件。 - 子任务 1（12 分）：$N \leq 5 000$，树是一条链，且节点 $1$ 是链的一个端点。 - 子任务 2（20 分）：$N \leq 300 000$，树是一条链，且节点 $1$ 是链的一个端点。 - 子任务 3（7 分）：$N \leq 20$； - 子任务 4（22 分）：$N \leq 5000$； - 子任务 5（39 分）：没有其他额外限制。