P10760 [BalticOI 2024] Portal

翻译自 [BalticOI 2024 Day1 T2](https://boi2024.lmio.lt/tasks/d1-portal-statement.pdf)。

你在和你的朋友玩一个恶作剧，朋友初始在 $(0,0)$ 位置，每个格子都有颜色，有 $N$ 个传送门，当你的朋友进入某个传送门之内时，会等概率地随机到 $N$ 个传送门其中之一（可能传送到原本的门，如果 $(0,0)$ 有传送门也要传送）。 可惜的是，你的朋友并不知道有传送门的存在，他只会根据他所走的格子确定他所在的格子与其颜色，你需要保证无论他怎么走，他所看到的格子颜色永远与他认为的格子颜色一样。 你可以随意染色，但是请最大化颜色数量，不难发现涂成一个颜色总是最小的解。

第一行一个整数 $N$，表示有 $N$ 个传送门。 接下来 $N$ 行，每行两个整数 $(x_i,y_i)$，表示传送门的坐标。

输出一个数表示你最大使用颜色的数量，如果可以使用无数种，输出 $-1$。

| 子任务编号 | 特殊性质 | 分值 | | :-----------: | :-----------: | :-----------: | | $1$ | $N \leq 2$ | $1$ | | $2$ | $N \leq 3$ | $10$ | | $3$ | 对于所有存在传送门的 $(x_1,y_1)$ 和 $(x_2,y_2)$，保证 $(x_1,y_2)$ 也存在传送门 | $10$ | | $4$ | $N \leq 100$ 且 $-100 \leq x_i,y_i \leq 100$ | $29$ | | $5$ | $N \leq 2000$ | $15$ | | $6$ | 无特殊性质 | $35$ | 对于全部数据，$1 \leq N \leq 10^5$，$-10^6 \leq x_i,y_i \leq 10^6$，且保证 $(x_i,y_i)$ 互不相同。 对于样例一，传送门被放置在 $(1,1)$、$(1,3)$ 和 $(3,2)$ 位置，如果你的朋友按照以下顺序移动：上、右、下、左。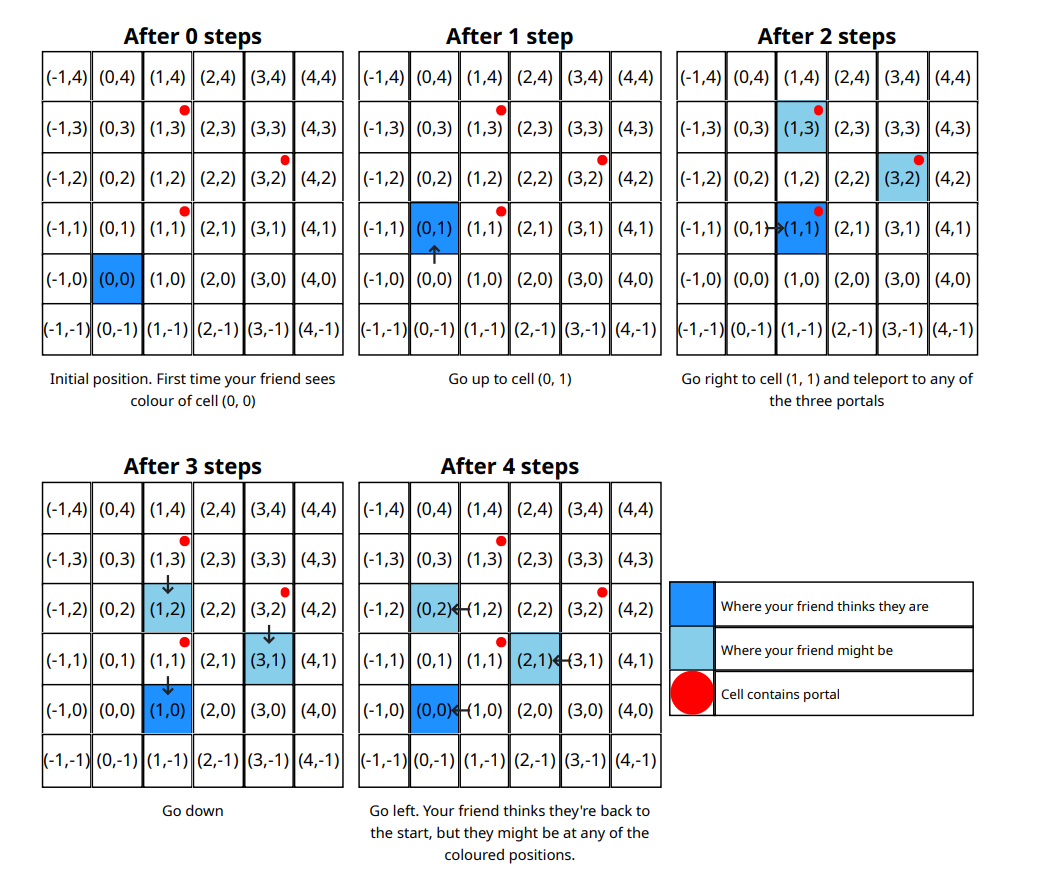  在移动序列结束后，你的朋友会认为他们回到了起始单元格$(0,0)$，但实际上他们也可能最终停在 $(0,2)$ 或 $(2,1)$。他们已经在开始时看到了 $(0,0)$ 单元格的颜色，所以如果现在他们看到不同的颜色，就会意识到必须有传送门的存在。我们不希望发生这种情况，所以我们必须为这三个单元格选择相同的颜色。 没有任何移动序列能让你的朋友认为他们最终停在 $(0,0)$ 单元格，而实际上他们却停在了 $(1,0)$ ，所以这些单元格可以放心地使用不同的颜色。 你可以看到下面例子中使用了 $4$ 种颜色的着色方案。对于这个例子来说，不可能使用超过 $4$ 种颜色。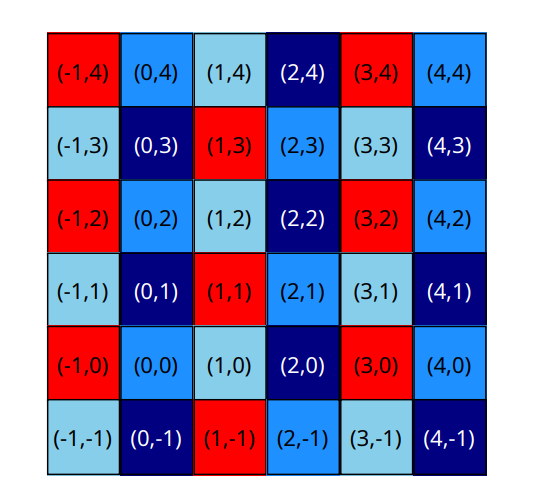  对于样例二，让我们考虑一个不同的例子，其中在单元格 $(0,0)$、$(0,1)$、$(1,0)$、$(0,-1)$ 和 $(-1,0)$ 处设有传送门。假设你的朋友试图通过先向右移动一次，然后向上移动三次来到达单元格 $(1,3)$。一种可能是，如果他们在一开始和每一步之后都被传送到那里，那么他们最终会到达单元格 $(0,0)$。如果你的朋友现在通过向下移动三次然后向左移动一次来回到他们认为的 $(0,0)$ 单元格，并且在这个过程中没有被从当前单元格传送走，他们最终会到达 $(-1,-3)$。你的朋友会第二次认为自己处于 $(0, 0)$ 单元格，并期望看到相同的颜色。所以你需要用相同的颜色给 $(-1,-3)$ 和 $(0, 0)$ 着色。 请注意，我们选择单元格 $(1,3)$ 作为起点并没有什么特别之处。你同样可以证明其他单元格必须与 $(0,0)$ 共享同一种颜色。