P10763 [BalticOI 2024] Tiles

翻译自 [BalticOI 2024 Day2 T2](https://boi2024.lmio.lt/tasks/d2-tiles-statement.pdf)。

有一个存在 $N$ 个顶点的大教堂，顶点坐标依次为 $(x_i,y_i)$，对于每个 $1 \leq i < N$，存在一条 $i$ 与 $i+1$ 之间的边，此外，还存在一条 $N$ 到 $1$ 的边。 大教堂每条边都与 $x$ 轴或 $y$ 轴平行。此外，大教堂是一个简单多边形，即： - 每个顶点恰好由两条边相交 - 任何一对边只能在顶点处相交 你有无数块 $2 \times 2$ 的瓷砖，你希望用这些瓷砖覆盖大教堂的大部分区域，具体来说，你想选择一条垂直线，并覆盖该线左侧的大教堂部分。对于任何整数 $k$，设 $L_k$ 为包含 $x$ 坐标等于 $k$ 的点的垂直线。对 $L_k$ 左侧大教堂部分的覆盖，是指在平面上放置一定数量的瓷砖，使得： - 多边形内部且 $x$ 坐标小于 $k$ 的每个点都被某块瓷砖覆盖 - 多边形外部或 $x$ 坐标大于 $k$ 的点都不被任何瓷砖覆盖 - 瓷砖的内部不重叠 大教堂中任何顶点的最小 $x$ 坐标为 $0$。我们设 $M$ 为大教堂中任何顶点的最大 $x$ 坐标。 请你求出最大的满足条件的 $k\ (0 \leq k \leq M)$，根据定义，一定存在答案为 $0$。

第一行两个整数 $N,M$。 接下来 $N$ 行，每行两个整数 $(x_i,y_i)$。这些顶点按照顺时针或逆时针顺序给出。

输出一个答案 $k$。

| 子任务编号 | 特殊性质 | 分值 | | :----------: | :----------: | :----------: | | $1$ | $N=4$ | $4$ | | $2$ | $N \leq 6$ | $9$ | | $3$ | $x_N=0,y_N=0$，对于 $1 \leq i \leq N-2$，$x_i \leq x_{i+1},y_i \geq y_{i+1}$ | $11$ | | $4$ | $M \leq 1000$ 且 $y_i \leq 1000$ | $19$ | | $5$ | $y_i$ 都为偶数 | $22$ | | $6$ | $x_i$ 都为偶数 | $25$ | | $7$ | 无特殊性质 | $10$ | 对于所有数据，$4 \leq N \leq 2 \times 10^5$，$1 \leq M \leq 10^9$，$0 \leq y_i \leq 10^9$，$\min(\{x_i\}) = 0,\max(\{x_i\}) = M$。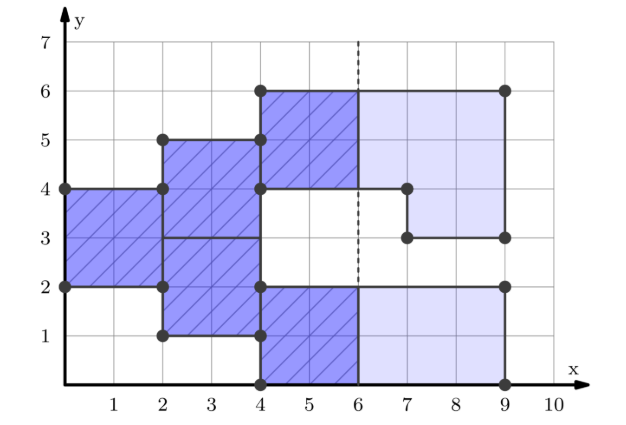 对于样例一，下面是对于 $k=2$ 的覆盖。  可以发现这是最大的情况了。 对于样例二，没有正值 $k$，使得 $L_k$ 左侧的教堂部分可以用瓷砖覆盖。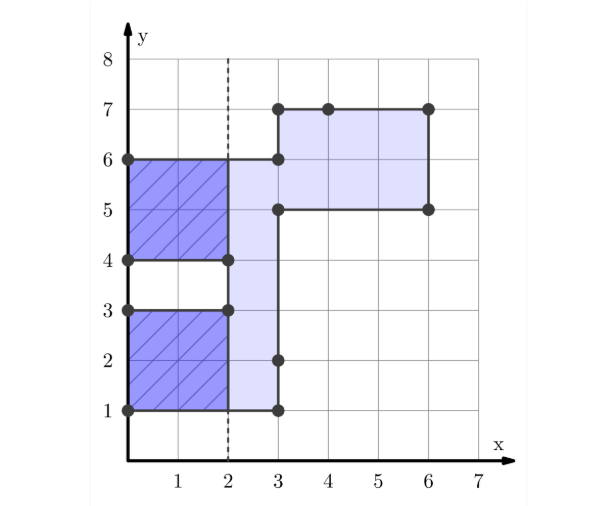 对于样例三，图示如下。