P10767 「CROI · R2」Under the Peach Tree of Longing II
Background
> Will you truly continue?
> Are you truly unwilling to give up?
> Is this truly meaningful?
Description
Fox demons organized a single-elimination tournament on Mount Tu. The $i$-th participant has strength $i$. In each match, two contestants compete, and the winner advances to the next round. To allow both stronger and weaker participants a chance to win, YaYa designed a special set of rules.
Specifically, there are $2^n$ participants in the tournament. Each match follows one of two predetermined rules:
- **Rule 1**: The stronger participant wins.
- **Rule 2**: The weaker participant wins.
YaYa will ask you $m$ queries. For a bracket with fixed match rules (but unknown initial participant placement), determine whether the $a$-th participant can advance to the $b$-th round. Output `Yes` if possible, otherwise `No`. Notably, if a participant becomes the champion, they are considered to have advanced to the $(n+1)$-th round.
The figure below shows an example bracket with fixed match rules but unknown participant placement. Matches marked with $\max$ follow Rule 1 (stronger wins), while those marked with $\min$ follow Rule 2 (weaker wins).
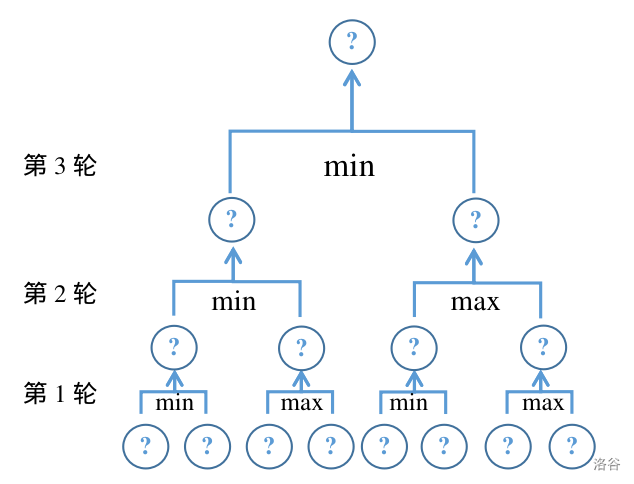
Input Format
The first line contains two integers $n$ and $m$, as described.
The next $n$ lines describe the bracket rules:
- The $i$-th line contains $2^{i-1}$ integers representing the rules for matches in the $(n-i+1)$-th round (from left to right). Here, `1` denotes Rule 1, and `2` denotes Rule 2.
The next $m$ lines each contain two integers $a$ and $b$, representing a query.
Output Format
Output $m$ lines, each containing `Yes` or `No` as the answer to the corresponding query.
Explanation/Hint
**【Sample Explanation】**
The sample bracket matches the figure in the problem description.
To allow the 6th participant to reach the second round, or the 7th participant to reach the third round, participants can be arranged as $\{1,2,3,4,7,8,5,6\}$. The specific match outcomes are shown below:
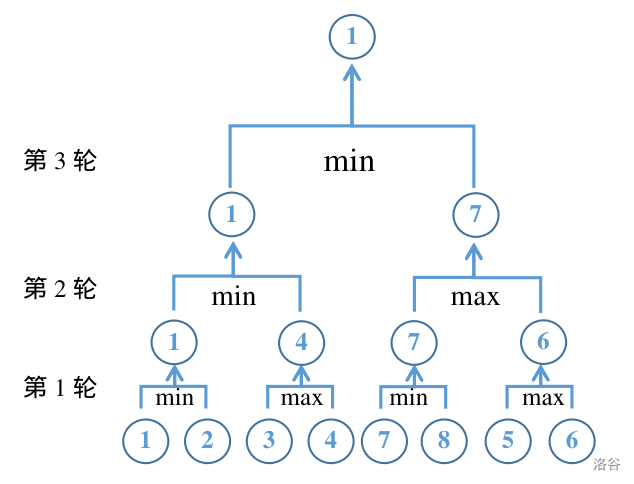
It is impossible for the 8th participant to reach the 4th round (i.e., become champion).
**【Data Range】**
**This problem uses bundled tests.**
- Subtask 0 (20 points): $n \leq 3$, $m \leq 20$.
- Subtask 1 (10 points): For all queries, $b \leq 2$.
- Subtask 2 (10 points): All matches follow Rule 1.
- Subtask 3 (20 points): All matches in the same round follow the same rule.
- Subtask 4 (40 points): No additional constraints.
For all test cases: $1 \leq a \leq 2^n$, $1 \leq b \leq n+1$, $1 \leq 2^n, m \leq 10^6$.