「CROI · R2」夏风与树

刺眼的阳光把大地烤得炽热，小 B 走在街上，迎面吹来一阵清风，路旁郁郁葱葱的树叶沙沙地摇晃着。 “夏风扫过树叶的声音就像下雨一样呢。”

Alice 和 Bob 在种树，同时，他们决定玩一个游戏。 Alice 拥有 $1\sim n$ 号结点，Bob 拥有 $(n+1)\sim 2n$ 号结点，这 $2n$ 个结点的权值恰好构成一个**排列** $a$，其中 $a_i$ 为 $i$ 号点上的权值。 首先，他们约定 $1$ 号点为树根。 然后，由 Alice 为 $2\sim n$ 号点决定父亲，其中 $i$ 号点的父亲只能在 $1\sim(i-1)$ 中选择。 接下来，由 Bob 为 $(n+1)\sim 2n$ 号点决定父亲，其中 $i$ 号点的父亲只能在 $0\sim(i-1)$ 中选择。$0$ 号点不在他们的树上，也就是说，Bob 的结点不一定要与这颗树连通。 最后，Alice 会从 $1$ 号点开始，对这棵树进行深度优先搜索，同时她会维护一个序列，搜索过程中，每遇到一个没访问过的点就将它上面的**权值**加入序列末尾。 Alice 希望最终序列的字典序尽可能小，Bob 希望最终序列的字典序尽可能大，并且他们二人都会采取最优策略。现在 Bob 请求你告诉他，最终序列会是什么样。 以下是关于字典序的定义： - 对于一个长度为 $n$ 的序列 $a$，若 $i>n$，约定 $a_i=-\infty$。 - 对于两个序列 $a, b$，我们定义 $a$ 的字典序小于 $b$ 当且仅当存在 $i\ge 1$，使得 $\forall 1 \leq j < i$，$a_j = b_j$，且 $a_i < b_i$。

**在本题的部分测试点中，Bob 会把 Alice 在第一步中决定好的 $2\sim n$ 号结点的父亲告诉你。** 第一行一个整数 $t$，表示子任务编号。特别地，样例的子任务编号为 $0$。 第二行一个正整数 $n$。 第三行 $2n$ 个正整数，表示排列 $a$。 第四行 $(n-1)$ 个整数，若该子任务拥有特殊性质 A，则表示 $2\sim n$ 号结点的父亲，否则这 $(n-1)$ 个整数都为 $0$。

一行，表示最终序列。

0
5
10 5 1 8 4 3 7 6 2 9
1 1 1 3

10 1 4 9 7 6 5 8 3 2

0
4
7 2 4 1 5 6 3 8
0 0 0

7 1 8 2 4 6 5 3

0
4
2 7 6 4 5 8 1 3
0 0 0

2 4 8 6 7 5 3

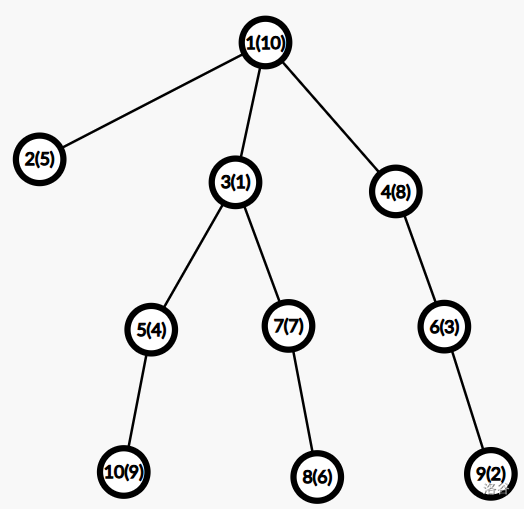
样例 #1 中，一种可能的最终树，数字为编号，括号内为权值：  ### 数据范围 | 子任务 | 分值 | $n$ | 特殊性质 | | :----------: | :----------: | :----------: | :----------: | | $1$ | $10$ | $\le 4$ |无 | | $2$ | $10$ | $\le 10^5$ |B| | $3$ | $30$ | $\le 10^5$ |A | | $4$ | $20$ | $\le 3000$ |无 | | $5$ | $30$ | $\le 10^5$ |无 | 特殊性质 A：输入中给定一种 Alice 的最优决策中 $2\sim n$ 号结点的父亲。 特殊性质 B：$a_{n+1}\sim a_{2n}$ 构成 $1\sim n$ 的一个排列。 对于 $100\%$ 的数据，$1\le n\le 10^5$，保证序列 $a$ 是一个 $1\sim 2n$ 的排列。