P10770 「CROI · R2」Summer Wind and Trees

The glaring sunlight scorched the earth. As Little B walked down the street, a cool breeze blew towards him, rustling the lush green leaves by the roadside. "The sound of the summer wind sweeping through the leaves is just like the sound of rain."

Alice and Bob are planting trees while playing a game. Alice owns nodes $1\sim n$, and Bob owns nodes $(n+1)\sim 2n$. The weights of these $2n$ nodes form a **permutation** $a$, where $a_i$ is the weight of node $i$. First, they agree that node $1$ is the root of the tree. Then, Alice decides the parent for nodes $2\sim n$, where the parent of node $i$ must be chosen from $1\sim (i-1)$. Next, Bob decides the parent for nodes $(n+1)\sim 2n$, where the parent of node $i$ can be chosen from $0\sim (i-1)$. Node $0$ is not part of their tree, meaning Bob's nodes do not need to be connected to this tree. Finally, Alice will perform a depth-first search starting from node $1$. During this process, she maintains a sequence: whenever she encounters an unvisited node, she appends its **weight** to the end of the sequence. Alice wants the lexicographical order of the final sequence to be as small as possible, while Bob wants it to be as large as possible. Both will adopt optimal strategies. Now Bob asks you to determine what the final sequence will be. Definitions related to lexicographical order: - For a sequence $a$ of length $n$, if $i > n$, we define $a_i = -\infty$. - For two sequences $a$ and $b$, we say $a$ is lexicographically smaller than $b$ if there exists an $i \ge 1$ such that for all $1 \leq j < i$, $a_j = b_j$, and $a_i < b_i$.

**In some test cases of this problem, Bob will provide you with the parents of nodes $2\sim n$ determined by Alice in the first step.** The first line contains an integer $t$, representing the subtask number. Notably, the sample input has subtask number $0$. The second line contains a positive integer $n$. The third line contains $2n$ positive integers, representing the permutation $a$. The fourth line contains $(n-1)$ integers. If the subtask has Special Property A, these integers represent the parents of nodes $2\sim n$. Otherwise, all $(n-1)$ integers are $0$.

A single line representing the final sequence.

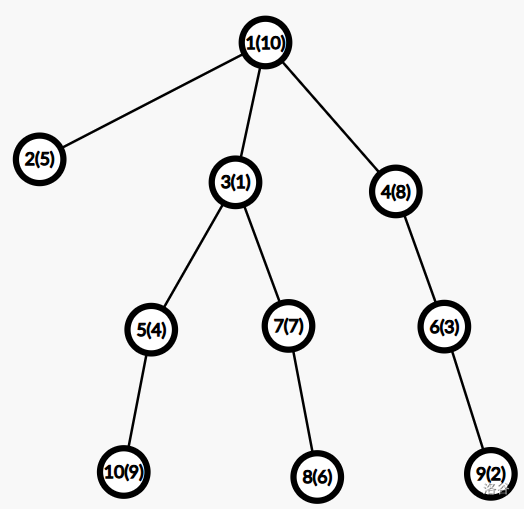
In Sample #1, a possible final tree is shown (numbers are node IDs, values in parentheses are weights):  ### Data Range | Subtask | Points | $n$ | Special Properties | | :-----: | :----: | :-----: | :----------------: | | $1$ | $10$ | $\le 4$ | None | | $2$ | $10$ | $\le 10^5$ | B | | $3$ | $30$ | $\le 10^5$ | A | | $4$ | $20$ | $\le 3000$ | None | | $5$ | $30$ | $\le 10^5$ | None | Special Property A: The input provides the parents of nodes $2\sim n$ under one of Alice's optimal strategies. Special Property B: $a_{n+1}\sim a_{2n}$ form a permutation of $1\sim n$. For $100\%$ of the data: $1 \le n \le 10^5$, and the sequence $a$ is guaranteed to be a permutation of $1\sim 2n$.