【MX-J1-T3】『FLA - III』Anxiety

原题链接：<https://oier.team/problems/J1C>。 --- I came. I saw. I had anxiety. I left.

给定一棵拥有 $2^n-1$ 个节点的二叉树，节点 $i$ 的权值为 $w_i$，节点 $1$ 为根节点。对于所有非根节点 $i$ 都有一条双向边连接节点 $i$ 和节点 $\left\lfloor \frac{i}{2} \right\rfloor$。请注意 $\left\lfloor X \right\rfloor$ 表示不大于 $X$ 的最大整数。 定义节点 $u,v$ 的距离为从节点 $u$ 到节点 $v$ 最少需要经过的边数。给定 $m$ 组询问，第 $i$ 组询问给定三个正整数 $x_i,y_i,k_i$，你需要输出树上与 $x_i,y_i$ 两个节点的距离都不超过 $k_i$ 的节点的权值之和。

第一行输入两个正整数 $n,m$。 第二行输入 $2^n-1$ 个正整数，第 $i$ 个正整数为 $w_i$。 接下来 $m$ 行，第 $i$ 行输入三个正整数 $x_i,y_i,k_i$。

输出 $m$ 行，每行一个整数，第 $i$ 行的整数表示第 $i$ 组询问的答案。

3 3
1 1 1 1 1 1 1
3 4 2
5 4 6
3 2 2

2
7
3

4 5
3 4 10 7 1 6 10 6 16 5 3 16 6 2 9
1 4 6
4 2 1
1 14 5
6 13 3
11 15 2

104
11
74
51
0

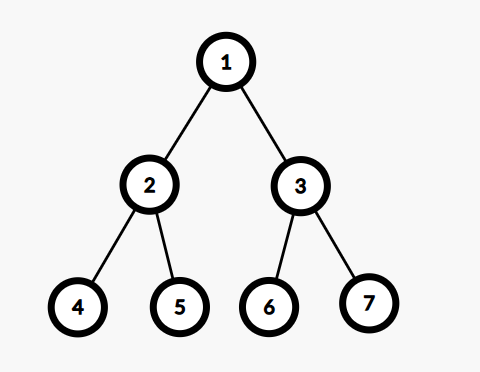
**「样例解释 #1」**  对于第一组询问，满足条件的节点有 $1,2$，权值和为 $2$。 对于第二组询问，满足条件的节点有 $1,2,3,4,5,6,7$，权值和为 $7$。 对于第三组询问，满足条件的节点有 $1,2,3$，权值和为 $3$。 **「数据范围」** |测试点编号|$n \leq$|$m \leq$|$k_i \leq$|$w_i \leq$| |:-:|:-:|:-:|:-:|:-:| |$1$|$2$|$5$|$5$|$10$| |$2 \sim 3$|$10$|$1000$|$1000$|$1000$| |$4 \sim 5$|$18$|$2 \times 10^5$|$5$|$10^9$| |$6 \sim 7$|$18$|$2 \times 10^5$|$10^9$|$1$| |$8 \sim 10$|$18$|$2 \times 10^5$|$10^9$|$10^9$| 对于 $100\%$ 的数据，$2 \leq n \leq 18$，$1 \leq m \leq 2 \times 10^5$，$1 \leq x_i,y_i \leq 2^n-1$，$1 \leq k_i \leq 10^9$，$1 \leq w_i \leq 10^9$，$x_i \neq y_i$。节点的编号是从 $1$ 到 $2^n-1$ 的整数。