P10803 [CEOI 2024] 文本编辑器

**题目译自 [CEOI 2024](https://ceoi2024.fi.muni.cz/) Day1 T3「[Text editor](https://ceoi2024.fi.muni.cz/page/tasks/statements/editor.pdf)」** 罗伯特正在参加 2024 年 CEOI 编程竞赛。他几乎完成了当天最难的一道题的代码，而且他确信能拿满分！但问题出在一个小小的细节上：他打错了一个字！更糟糕的是，他从 2008 年就开始使用的那只心爱鼠标彻底罢工了，一点反应也没有。因此，他只能用键盘上的方向键移动光标去找到那个错别字。 罗伯特的程序有 $N$ 行，每行的长度分别为 $l_1, l_2, \ldots , l_N$。罗伯特总是以空行作为程序的结尾，所以 $l_N = 0$。光标可以放在两个字符之间，也可以放在行的开头或结尾。因此，第 $i$ 行有 $l_i + 1$ 个可用的光标位置（称为列），编号从 $1$ 到 $l_i + 1$。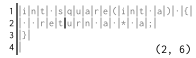例如，下面是光标位于第 $2$ 行第 $6$ 列的情况：  罗伯特想把光标从第 $s_l$ 行的第 $s_c$ 列移动到第 $e_l$ 行的第 $e_c$ 列。他想求出最少需要的按键次数。 水平方向键的使用比较简单。按下 **左键** 会将光标移动到前一列，除非光标位于行首，则会移动到前一行的行尾。类似地，按下 **右键** 会将光标移动到后一列，或者如果光标位于行尾，则会移动到下一行的行首。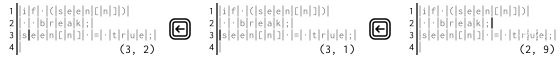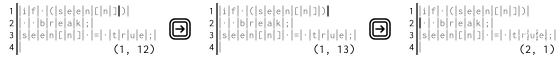 例如，**左键** 的移动可以像这样：  而 **右键** 的移动可以像这样：  在文件的最开头按下 **左键** 或在文件的最结尾按下 **右键** 都不会有任何效果。 垂直方向键的使用稍微复杂一些。按下 **上键** 会将光标移动到上一行，按下 **下键** 会将光标移动到下一行，列数不会改变。但是，如果这样会使光标超出新行的结尾，光标则会跳到该行末尾。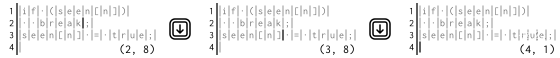 例如，**上键** 的移动可以像这样：  而 **下键** 的移动可以像这样：  如果按下 **上键** 或 **下键** 会把光标移动到不存在的行，则光标根本不会移动。

输入的第一行包含一个整数 $N$，表示罗伯特程序的行数。 第二行包含两个空格隔开的整数 $s_l$ 和 $s_c$，表示初始光标位置。 类似地，第三行包含两个空格隔开的整数 $e_l$ 和 $e_c$，表示目标光标位置。 第四行包含 $N$ 个空格隔开的整数 $l_1, l_2, \ldots , l_N$，表示每行的长度。

输出一行包含一个整数，表示将光标从 $(s_l, s_c)$ 移动到 $(e_l, e_c)$ 最少的按键次数。

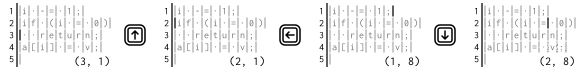
**样例解释 1** 罗伯特可以通过按顺序按 **上键**、**左键** 和 **下键**三个键来将光标移动到目标位置：  或者，他也可以通过按 **左键**、**上键** 和 **下键** 来同样快速地将光标移动到目标位置。 **样例解释 2** 可以很容易地证明，不可能使用最多两个按键到达目标位置。 最短的可能按键序列是按两次 **下键** 然后按十四次 **右键**。 对于所有输入数据，满足： - $1 \leq N \leq 10^6$ - $0 \leq l_i \leq 10^9\ (1\leq i\leq n)$ - $l_N = 0$ - $1 \leq s_l, e_l \leq N$ - $1 \leq s_c \leq l_{s_l} + 1$ - $1 \leq e_c \leq l_{e_l} + 1$ 详细子任务附加限制及分值如下表所示。 | 子任务 | 附加限制 | 分值 | | :--: | :--: | :--: | | $1$ | $N \leq 2$ | $5$ | | $2$ | $N \leq 1\,000, l_i \leq 5\,000\ (1 \leq i \leq N)$| $14$ | | $3$ | $N \leq 1\,000$ | $26$ | | $4$ | $l_i = l_j\ (1 \leq i, j \leq N - 1)$ | $11$ | | $5$ | 无附加限制| $44$ |