P1081 [NOIP 2012 Senior] Driving Trip

Little $\text{A}$ and Little $\text{B}$ decide to travel during the holidays. They number the cities from $1$ to $n$, where a city with a smaller index lies to the west of a city with a larger index. The altitudes of all cities are distinct. Let the altitude of city $i$ be $h_i$. The distance $d_{i,j}$ between city $i$ and city $j$ is exactly the absolute difference of their altitudes, i.e., $d_{i,j}=|h_i-h_j|$. During the trip, Little $\text{A}$ and Little $\text{B}$ take turns driving. Little $\text{A}$ drives on the first day, and they alternate each subsequent day. They plan to choose some city $s$ as the starting point, always drive eastward, and end the trip after driving at most $x$ kilometers in total. Little $\text{A}$ and Little $\text{B}$ have different driving styles. Little $\text{B}$ always chooses the nearest city in the forward (east) direction as the destination, while Little $\text{A}$ always chooses the second nearest city in the forward direction (note: in this problem, if the distances from the current city to two cities are the same, the city with the lower altitude is considered closer). If either person cannot choose a destination according to their rule, or if reaching the chosen destination would cause the total distance to exceed $x$ kilometers, the trip ends. Before setting off, Little $\text{A}$ wants to know two things: 1. For a given $x=x_0$, from which city should they start so that the ratio of the total distance driven by Little $\text{A}$ to that driven by Little $\text{B}$ is minimized (if Little $\text{B}$'s total distance is $0$, the ratio is considered infinite, and all infinities are regarded equal). If multiple starting cities yield the same minimum ratio, output the city with the highest altitude. 2. For any given $x=x_i$ and starting city $s_i$, the total distance driven by Little $\text{A}$ and the total distance driven by Little $\text{B}$.

- The first line contains an integer $n$, the number of cities. - The second line contains $n$ integers separated by spaces, representing the altitudes of cities $1$ through $n$, i.e., $h_1,h_2,\dots,h_n$, and all $h_i$ are distinct. - The third line contains an integer $x_0$. - The fourth line contains an integer $m$, the number of given pairs $(s_i,x_i)$. - Each of the next $m$ lines contains $2$ integers $s_i$ and $x_i$, indicating that the trip starts from city $s_i$ and the total distance is at most $x_i$ kilometers.

Output $m+1$ lines. - The first line contains an integer $s_0$, indicating that for the given $x_0$, starting from city $s_0$ minimizes the ratio of the total distance driven by Little $\text{A}$ to that driven by Little $\text{B}$. - Each of the next $m$ lines contains $2$ integers separated by a space, indicating, for the given $s_i$ and $x_i$, the total distance driven by Little $\text{A}$ and by Little $\text{B}$, respectively.

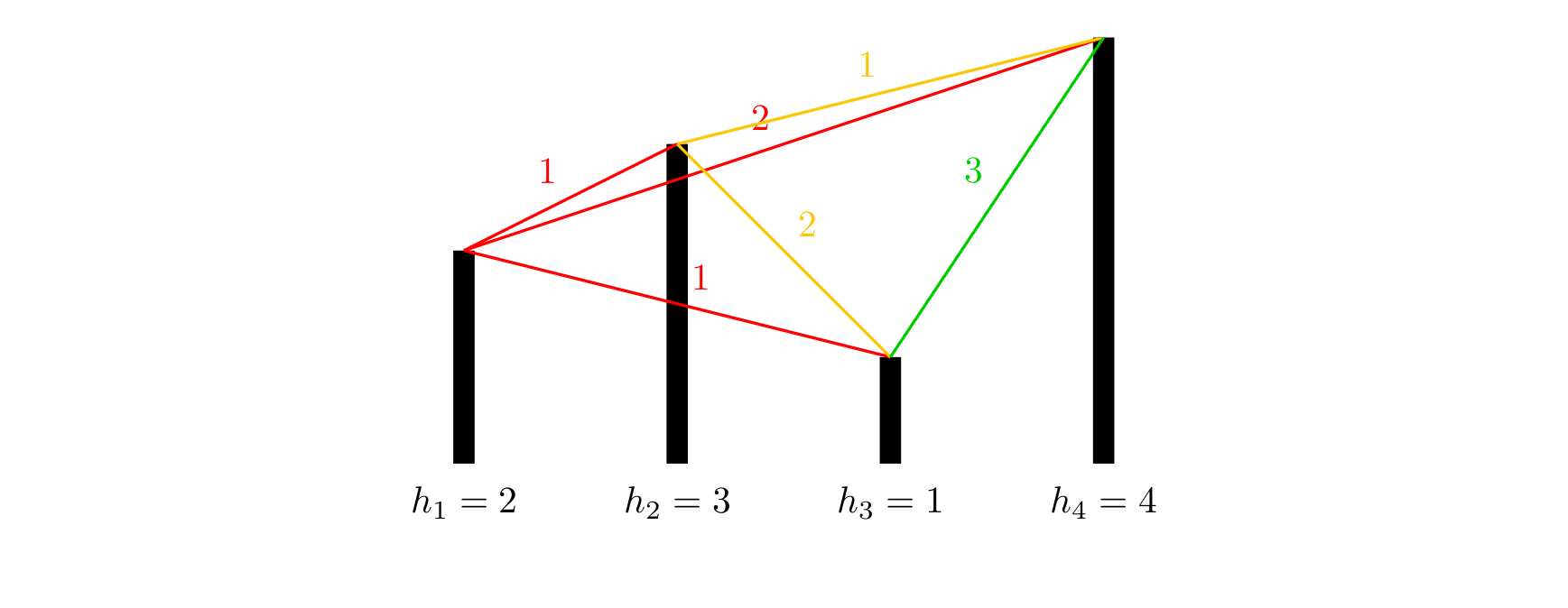
[Explanation for Sample 1]  The altitudes of the cities and the distances between pairs of cities are as shown above. If starting from city $1$, the reachable cities ahead are $2,3,4$, with distances from city $1$ being $1,1,2$, respectively. However, since the altitude of city $3$ is lower than that of city $2$, we consider city $3$ closer to city $1$, and city $2$ the second closest, so Little $\text{A}$ goes to city $2$. After reaching city $2$, the reachable cities ahead are $3,4$, with distances $2,1$, respectively, so city $4$ is closer to city $2$; therefore Little $\text{B}$ goes to city $4$. After reaching city $4$, there are no reachable cities ahead, so the trip ends. If starting from city $2$, the reachable cities ahead are $3,4$, with distances $2,1$, respectively. Since city $3$ is the second closest to city $2$, Little $\text{A}$ goes to city $3$. After reaching city $3$, the only remaining forward city is $4$, so city $4$ is the closest to city $3$. However, going to city $4$ would make the total distance $2+3=5>3$, so Little $\text{B}$ ends the trip at city $3$. If starting from city $3$, the only reachable city ahead is $4$. Since there is no second closest city to city $3$, the trip ends before it starts. If starting from city $4$, there are no reachable cities ahead, so the trip ends before it starts. [Explanation for Sample 2] When $x=7$, if starting from city $1$, the route is $1 \to 2 \to 3 \to 8 \to 9$. Little $\text{A}$ travels $1+2=3$, and Little $\text{B}$ travels $1+1=2$. (At city $1$, the cities closest to Little $\text{A}$ are $2$ and $6$, but city $2$ has a higher altitude and is regarded as the second closest to city $1$, so Little $\text{A}$ ultimately chooses city $2$. After reaching $9$, Little $\text{A}$ can only go to city $10$, and there is no second choice, so no decision can be made and the trip ends.) If starting from city $2$, the route is $2 \to 6 \to 7$. Little $\text{A}$ and Little $\text{B}$ travel $2$ and $4$, respectively. If starting from city $3$, the route is $3 \to 8 \to 9$. Little $\text{A}$ and Little $\text{B}$ travel $2$ and $1$, respectively. If starting from city $4$, the route is $4 \to 6 \to 7$. Little $\text{A}$ and Little $\text{B}$ travel $2$ and $4$, respectively. If starting from city $5$, the route is $5 \to 7 \to 8$. Little $\text{A}$ and Little $\text{B}$ travel $5$ and $1$, respectively. If starting from city $6$, the route is $6 \to 8 \to 9$. Little $\text{A}$ and Little $\text{B}$ travel $5$ and $1$, respectively. If starting from city $7$, the route is $7 \to 9 \to 10$. Little $\text{A}$ and Little $\text{B}$ travel $2$ and $1$, respectively. If starting from city $8$, the route is $8 \to 10$. Little $\text{A}$ and Little $\text{B}$ travel $2$ and $0$, respectively. If starting from city $9$, the route is $9$. Little $\text{A}$ and Little $\text{B}$ travel $0$ and $0$, respectively (the trip ends immediately). If starting from city $10$, the route is $10$. Little $\text{A}$ and Little $\text{B}$ travel $0$ and $0$, respectively. Starting from city $2$ or city $4$ yields the same minimum ratio of Little $\text{A}$'s total distance to Little $\text{B}$'s total distance, but city $2$ has a higher altitude, so the first line of the output is $2$. Constraints - For $30\%$ of the testdata: $1 \le n \le 20, 1 \le m \le 20$. - For $40\%$ of the testdata: $1 \le n \le 100, 1 \le m \le 100$. - For $50\%$ of the testdata: $1 \le n \le 100, 1 \le m \le 1000$. - For $70\%$ of the testdata: $1 \le n \le 1000, 1 \le m \le 10^4$. - For $100\%$ of the testdata: $1 \le n,m \le 10^5$, $-10^9 \le h_i≤10^9$, $1 \le s_i \le n$, $0 \le x_i \le 10^9$. The testdata guarantees that $h_i$ are pairwise distinct. Translated by ChatGPT 5