P10820 [EC Final 2020] Tube Master III

Prof. Pang is playing ``Tube Master``. The game field is divided into $n \times m$ cells by $(n + 1) \times m$ horizontal tubes and $n \times (m + 1)$ vertical tubes. The product $n m$ is an $\textbf{even}$ number. There are $(n + 1) (m + 1)$ crossings of the tubes. The 2D coordinate of the crossings are $(i, j)$ ($1\le i\le n+1$, $1\le j\le m+1$). We name the crossing with coordinate $(i, j)$ as crossing $(i, j)$. We name the cell whose corners are crossings $(i, j), (i+1, j), (i, j+1), (i+1, j+1)$ as cell $(i, j)$ for all $1\le i\le n$, $1\le j\le m$. Additionally, each cell $(i, j)$ contains an integer ${count}_{i, j}$.  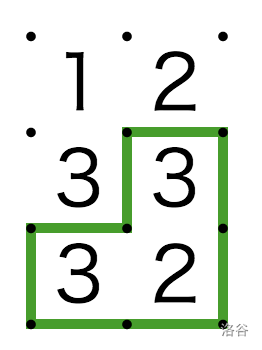The above figure shows a game field with $n = 3, m = 2$ (the third sample). Prof. Pang decides to use some of the tubes. However, the game poses several weird restrictions. - Either $0$ or $2$ tubes connected to each crossing are used. - There are exactly ${count}_{i, j}$ turning points adjacent to cell $(i, j)$. A turning point is a crossing such that exactly $1$ horizontal tube and exactly $1$ vertical tube connected to it are used. A turning point $(x, y)$ is adjacent to cell $(i, j)$ if crossing $(x, y)$ is a corner of cell $(i, j)$. It costs $a_{i, j}$ to use the tube connecting crossings $(i, j)$ and $(i, j+1)$. It costs $b_{i, j}$ to use the tube connecting crossings $(i, j)$ and $(i+1, j)$. Please help Prof. Pang to find out which tubes he should use such that the restrictions are satisfied and the total cost is minimized.

The first line contains a single positive integer $T$ denoting the number of test cases. For each test case, the first line contains two integers $n$, $m$ ($1 \leq n, m \leq 100$) separated by a single space. The $i$-th of the following $n$ lines contains $m$ integers ${count}_{i, 1}, {count}_{i, 2}, \dots, {count}_{i, m}$ ($0 \leq {count}_{i, j} \leq 4$) separated by single spaces. The $i$-th of the following $n+1$ lines contains $m$ integers ${a}_{i, 1}, {a}_{i, 2}, \dots, {a}_{i, m}$ ($1 \leq {a}_{i, j} \leq 10^9$) separated by single spaces. The $i$-th of the following $n$ lines contains $m+1$ integers ${b}_{i, 1}, \mathit{b}_{i, 2}, \dots, {b}_{i, m+1}$ ($1 \leq {b}_{i, j} \leq 10^9$) separated by single spaces. It is guaranteed that $nm$ is an $\textbf{even}$ number and that the total sum of $nm$ over all test cases does not exceed $10^4$.

For each test case, output an integer that denotes the minimum cost. If there is no valid configuration, output $\texttt{-1}$ instead.