P10834 [COTS 2023] 题 Zadatak
题目背景
译自 [Izborne Pripreme 2023 (Croatian IOI/CEOI Team Selection)](https://hsin.hr/pripreme2023/) D2T3。$\texttt{1s,0.5G}$。
祝 NaCly_Fish 生日快乐!(2024.7.28)
题目描述
Jura 有 $N$ 个正方形,标号为 $1\sim N$,第 $i$ 个正方形边长为 $a_i$,且 $2\mid a_i$。起初,这些正方形都是黑色的。
Jura 决定花费他生命中的 $(N-1)$ 秒来玩这些正方形。在第 $i$ 秒时,Jura 将第 $x_i$ 和第 $y_i$ 个正方形合并成第 $(N+i)$ 个正方形(合并后,第 $x_i$ 和第 $y_i$ 个正方形不再存在)。
合并正方形时,将两个正方形的中心对齐,边缘平行对齐地摆在平面中。新的正方形的大小为合并的两个正方形中较大那个的大小;它的颜色是原来两个正方形颜色的「异或和」(黑+黑=白,白+白=白,黑+白=黑,白+黑=黑)。合并正方形的**代价**为,两个正方形合并前(但是已经按照刚才的要求摆好),正方形的交中,满足在两个正方形中均为黑色的区域的面积。
你需要输出每次合并操作的代价。
下图为正方形合并的示例:
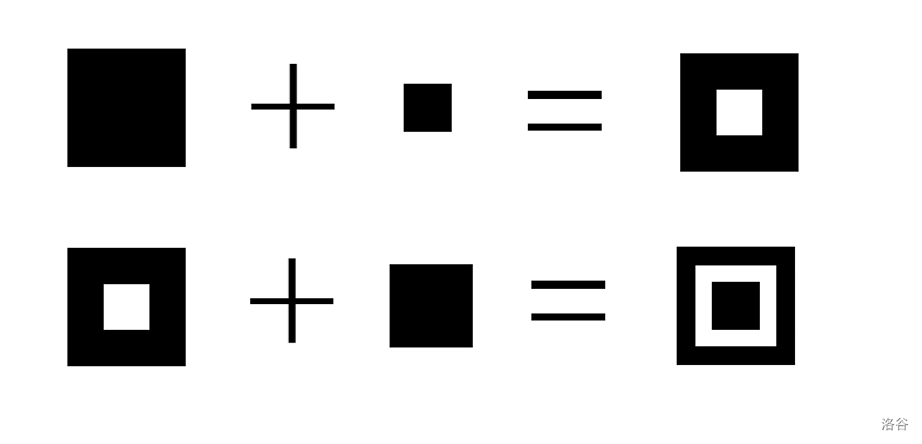
输入格式
第一行,一个正整数 $N$,表示正方形数量;
第二行,$N$ 个正整数,描述序列 $a$。
接下来 $(N-1)$ 行,每行两个正整数 $x_i,y_i$,描述一次操作。
输出格式
输出 $(N-1)$ 行,每行一个整数,表示操作的代价。
说明/提示
### 样例解释
样例 $1$ 的最后一个操作如图所示:

#### 数据范围
对于 $100\%$ 的数据,保证:
- $1\le N\le 10^5$;
- $2\le a_i\le 10^6$。
- $2\mid a_i$。
- $1\le x_i,y_i\le N+i-1$
- 操作前正方形存在,且 $x_i\neq y_i$。
| 子任务编号 | 分值 | 约束 |
|:-----:|:------:|:-------:|
| $1$ | $14$ | $N\le 5\, 000$ |
| $2$ | $25$ | $x_1=1,y_1=2$;$\forall 2\le i\le N-1$,$x_i=i+1,y_i=N+i-1$ |
| $3$ | $17$ | $\exists k\in \mathbb{N}$,使得 $2^k=N$;$x_i=2i-1,y_i=2i$ |
| $4$ | $21$ | $n\le 30\, 000$ |
| $5$ | $23$ | 无额外约束 |