『FLA - I』庭中有奇树

**[English statement.](/problem/U458239) You must submit your code at the Chinese version of the statement.**  某天晚上小 G 和小 Y 本打算激情 CF 但过掉两题就下班了，然后他们准备玩一个游戏。

给定一棵有 $n$ 个节点的无根树，边带权，树上有一个起始节点 $S$ 和一个终止节点 $T$。 有一枚可以沿着边在节点之间移动的棋子，它每次移动花费的硬币数量等于经过的边的权值。 如果当前棋子所在节点为 $u$ 且节点 $v$ 与节点 $u$ 之间连有一条权值为 $w$ 的边，小 G 就能花费 $w$ 个硬币把棋子移动到节点 $v$。游戏开始时棋子位于节点 $S$，我们的小 G 要控制棋子移动到节点 $T$。 由于曾经有人告诉小 G 玩某游戏不开挂等于没玩，小 G 决定开挂。他的外挂可以花费 $k$ 个硬币把棋子从当前节点传送到任意一个**没有和当前节点连边**的节点，小 G 只能用这个外挂至多一次。 正义的小 Y 不能坐视不管，在小 G 开始行动之前，小 Y 可以封锁至多 $m$ 条可能的传送路线。假设小 Y 封锁了从节点 $x$ 向节点 $y$ 的传送路线，小 G 把棋子从节点 $x$ 传送到节点 $y$ 花费的硬币数量就会变成 $10^9$。由于外挂功能强大，小 G 知道小 Y 都封锁了哪些路线。**请注意传送路线是单向的，封锁节点 $x$ 向节点 $y$ 的传送路线不影响小 G 从节点 $y$ 向节点 $x$ 传送。** 有趣的是，游戏中小 G 不仅负责控制棋子移动到节点 $T$，还想**最小化**花费的硬币数量；而小 Y 想要**最大化**小 G 花费的硬币数量。 如果两人都采取最优策略，小 G 总共会花掉多少硬币？

第一行输入五个整数 $n,m,k,S,T$。 接下来 $n-1$ 行，第 $i$ 行输入三个正整数 $u_i,v_i,w_i$ 表示节点 $u_i$ 和节点 $v_i$ 之间有一条边权为 $w_i$ 的边。

输出一行一个整数，表示在两人都采取最优策略的情况下小 G 花费的硬币数量。

4 2 2 1 2
2 3 6
4 1 6
3 1 8

14

9 7 4 1 6
3 8 7
6 8 6
6 7 4
2 5 3
3 2 2
3 9 12
2 1 2
8 4 11

12

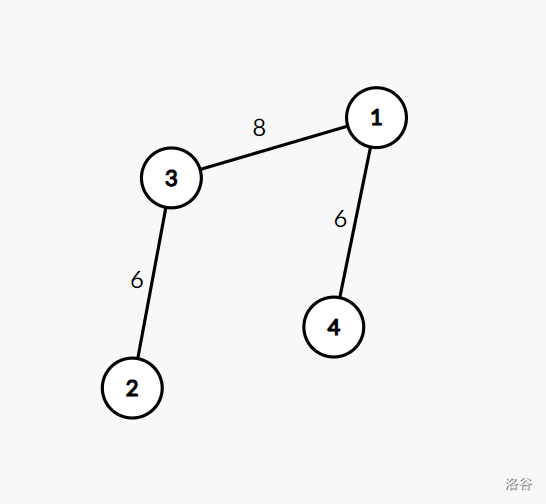
**「样例解释 #1」**  给出一种可能发生的情况：小 Y 封锁节点 $1$ 向节点 $2$ 的传送路线和节点 $4$ 向节点 $2$ 的传送路线。 小 G 控制棋子从初始节点到达节点 $4$，从节点 $4$ 传送到节点 $3$ 后再到达终止节点，总共花费 $14$ 个硬币。 **「数据范围」** **本题采用捆绑测试。** |Subtask|$n\leq$|$m \leq$|特殊性质|分值| |:---:|:---:|:---:|:---:|:---:| |**#1**|$1000$|$10^5$|无|$10$| |**#2**|$10^5$|$0$|无|$10$| |**#3**|$10^5$|$10^5$|无|$10$| |**#4**|$10^5$|$10^9$|A|$15$| |**#5**|$10^5$|$10^9$|B|$15$| |**#6**|$10^5$|$10^9$|无|$40$| - 特殊性质 A：保证 $k=10^9$。 - 特殊性质 B：保证 $k=0$。 对于所有测试数据，$2 \leq n \leq 10^5$，$0 \leq m,k \leq 10^9$，$1 \leq S,T,u_i,v_i \leq n$，$1 \leq w_i \leq 10^9$，$S \neq T$，$u_i \neq v_i$。节点的编号是从 $1$ 到 $n$ 的整数。 2024 年 8 月 4 日：将样例置于 Subtask #0。