P10838 『FLA - I』Magical Tree in the Courtyard

 > Glz: The upper bound is 4e10\ > Ycy: Wow\ > Ycy: Ancestor One night, Glz and Ycy participated in a Codeforces contest. However, they only solved two problems, and after that they decided to play a game.

In the game, Glz is given an unrooted tree with $n$ nodes, with a starting node $S$ and a destination node $T$. Each of the edges has an integer weight. There is a piece that can be moved between nodes along the edges, with each move costing a number of coins equal to the weight of the edge it passes through. That is, if there exists an edge connecting nodes $x$ and $y$ with an edge of weight $w$, then Glz can choose to move the piece from $x$ to $y$, paying $w$ coins. At the beginning of the game the piece is at node $S$. Glz needs to make the piece at node $T$ eventually after some moves. Since Glz was once told that playing a game without using a plug-in is the same as not playing, Glz decides to use a plug-in. Using this plug-in he can spend $k$ coins on moving a piece from the current node to any node **not adjacent** to the current node. However, Glz can only use this plug-in at most once. The righteous Ycy cannot sit idly by. Before Glz makes his move, Ycy can block up to $m$ possible teleportation routes. If Ycy blocks the teleportation route from node $x$ to node $y$, the number of coins that it takes for Glz to teleport a piece from node $x$ to node $y$ becomes exactly $10^9$ coins. Due to the power of the plug-in, Glz knows which routes Ycy has blocked after his moving process begins. **Note that the blocking procedure is unidirectional, that is, blocking the teleportation route from node $x$ to node $y$ does not affect Glz's teleportation from node $y$ to node $x$.** Interestingly, during the game, Glz wants to **minimize** the number of coins spent, while Ycy is trying to **maximize** the number of coins spent. If both of them adopt their optimal strategy, how many coins will Glz spend in total?

The first line of input contains five integers $n$, $m$, $k$, $S$ and $T$ — the number of nodes on the tree, the maximum teleportation routes that can be blocked, the coins that using the plug-in costs, the index of the starting node and the index of the destination node. Then $n - 1$ lines follow, each line contains three integers $u_i$, $v_i$, $w_i$, representing an edge on the tree connecting nodes $u_i$ and $v_i$, with a weight of $w_i$.

Output a single line containing an integer, which denotes the coins that Glz would spend, in the case where both of them adopt their optimal strategy.

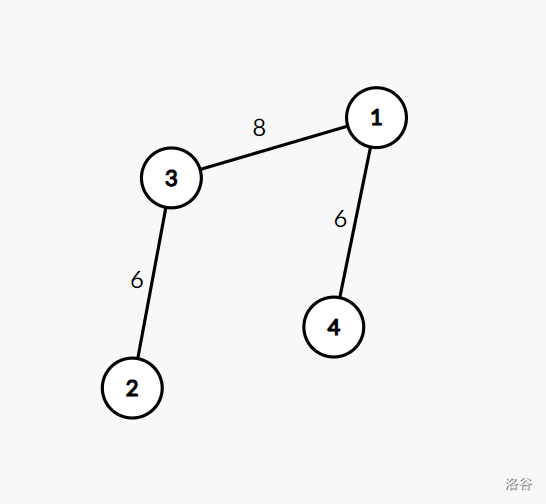
**「Sample Explanation #1」**  In a possible scenario, Ycy blocks the teleportation routes from node $1$ to node $2$ and from node $4$ to node $2$. Glz moves the piece from node $1$ to node $4$, and from node $4$ he teleports to node $3$, and then moving to node $2$, spending a total of $14$ coins. **「Constraints」** **Subtasks are used in this problem.** | Subtask Id | $n \leq$ | $m \leq$ | Special Properties | Score | | :--------: | :------: | :------: | :--------------: | :---: | | **#1** | $1000$ | $10^5$| No | $10$ | | **#2** | $10^5$ | $0$ | No | $10$ | | **#3** | $10^5$ | $10^5$ | No | $10$ | | **#4** | $10^5$ | $10^9$ | A | $15$ | | **#5** | $10^5$ | $10^9$ | B | $15$ | | **#6** | $10^5$ | $10^9$ | No | $40$ | - Special Property A: $k = 10^9$. - Special Property B: $k = 0$. For all tests, it is guaranteed that $2 \leq n \leq 10^5$, $0 \leq m,k \leq 10^9$, $1 \leq S,T,u_i,v_i \leq n$, $1 \leq w_i \leq 10^9$, $S \neq T$, $u_i \neq v_i$. Nodes are numbered from $1$ to $n$.