P10847 [EGOI 2024] Garden Decorations / 花园装饰（通信题无法评测）

Day 1 Problem D. 题面译自 [EGOI2024 gardendecoration](https://wiki.egoi2024.nl/tasks/gardendecoration/statement-isc.pdf)。翻译来自于 [ChatGPT](https://chatgpt.com/) 并进行人工校对，若有误请联系 [rui_er](https://www.luogu.com.cn/user/122461)。 7s 1GB **本题是一道通信题，你的程序会被多次执行。**

每天上学和回家的时候，Detje 都会沿着一条有 $N$ 栋房子的街道行走，这些房子从 $0$ 编号到 $N - 1$。目前，第 $i$ 号房子住着第 $i$ 号居民。为了换个环境，居民们决定互换房子。将要搬进第 $i$ 号房子的人是目前住在第 $a_i$ 号房子的人。 每栋房子花园里都有一只鸟雕像。这些雕像有两种状态：它们的翅膀要么是**展开的**（像是在飞翔），要么是**闭合的**（像是在地上站立）。居民们对他们的鸟雕像的样子有很强的偏好。目前，第 $i$ 号房子前的鸟雕像是第 $i$ 号居民喜欢的状态。居民们拒绝搬到一个雕像未设置为他们喜欢的状态的房子里。Detje 想帮他们调整鸟雕像的状态，以便他们能够搬家。 为此，她做了以下事情：每次她沿着街道行走（无论是上学还是回家），她会逐个观察经过的鸟，并可能调整一些雕像（通过打开或闭合它们的翅膀）。由于她在学校和家里非常忙碌，**她不记得之前走过的鸟的状态**。幸运的是，她写下了 $a_0,a_1,\cdots,a_{N-1}$ 列表，所以她知道哪个居民要搬到哪里。 帮助 Detje 设计一个策略，告诉她应该调整哪些鸟雕像，以便将雕像调整到居民们喜欢的状态。她最多可以沿街道行走 60 次，但为了获得更高的分数，她应该减少行走的次数。 --- **交互方式** 本题是一道通信题，你的程序会被多次执行。 在每次运行中，你应首先读取一行包含两个整数 $w$ 和 $N$，分别是行走的索引和房子的数量。在程序的第一次运行中 $w = 0$，第二次运行中 $w = 1$，依此类推（下面会详细说明）。 在输入的第二行，有 $N$ 个整数 $a_0,a_1,\cdots,a_{N-1}$，表示将要搬进第 $i$ 号房子的人目前住在第 $a_i$ 号房子。$a_i$ 的值形成一个**排列**：即 $a_i$ 列表中每个数从 $0$ 到 $N - 1$ 都只出现一次。注意，居民可以选择不搬家，即 $a_i = i$ 是允许的。 居民们只会互换一次房子。这意味着对于一个固定的测试用例，$N$ 的值和 $a_i$ 列表在程序的所有运行中都是相同的。 **第一次运行。** 在程序的第一次执行中，$w = 0$。在这次运行中，你应输出一个整数 $W$（$0 \le W \le 60$），表示 Detje 想要沿街道走多少次。然后程序应退出。之后，程序将再次执行 $W$ 次。 **后续运行。** 在程序的下一次运行中，$w = 1$；再下一次中 $w = 2$；依此类推，直到最后一次运行，$w = W$。 在读取 $w, N$ 和 $a_0,a_1,\cdots,a_{N-1}$ 之后，Detje 开始沿街道行走。 - 如果 $w$ 是奇数，Detje 从家走到学校，她会按 $0, 1,\cdots, N - 1$ 的顺序经过房子。 你的程序现在应读取一行包含 $b_0$，它是当前第 $0$ 号房子前雕像的状态，$0$ 表示闭合，$1$ 表示展开。读取 $b_0$ 之后，你应输出一行，包含你想将 $b_0$ 设置为的新的状态，$0$ 或 $1$。 然后你的程序应读取一行包含 $b_1$，即第 $1$ 号房子前雕像的状态；并输出 $b_1$ 的新状态。对于所有 $N$ 栋房子，这个过程继续进行。Detje 经过最后一栋房子（即读取并写入 $b_{N-1}$）后，**你的程序应退出**。 **注意：你的程序只能在写入 $b_i$ 的新值后读取下一个 $b_{i+1}$ 的值。** - 如果 $w$ 是偶数，Detje 从学校走到家，她会按 $N - 1, N - 2,\cdots, 0$ 的顺序经过房子。即你从读取并写入 $b_{N-1}$ 开始，然后是 $b_{N-2}$，依此类推直到 $b_0$。 当 $w = 1$ 时，输入值 $b_0,b_1,\cdots,b_{N-1}$ 是鸟雕像的初始状态（也是居民们喜欢的状态）。当 $w > 1$ 时，输入的 $b_0,b_1,\cdots,b_{N-1}$ 值是上一次运行程序时设置的状态。 最终，在程序的最后一次运行后，对于所有 $i$，值 $b_i$ 必须等于初始的 $b_{a_i}$ 值，否则程序会被判定为 WA。 **详细信息。** 如果 $W + 1$ 次单独运行程序的总运行时间超过时间限制，程序会被判定为 TLE。 输出每一行后，请确保刷新标准输出；否则，程序可能会被判定为 TLE。在 Python 中，只要使用 `input()` 读取行，就会自动刷新。在 C++ 中，`cout

见【交互方式】部分。

见【交互方式】部分。

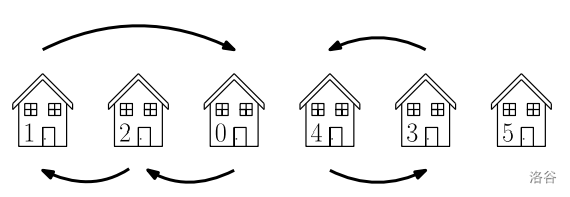
**样例解释** **题面中的三个样例对应同一个测试点的三次交互过程。** 在样例中，我们得到了以下房屋中的人们的排列：  样例程序第一次运行时（$w = 0$），它输出 $W = 2$，这意味着 Detje 将沿着街道走两次（并且程序将再运行两次）。在第一次行走之前，花园里的鸟的状态如下所示：  然后程序以 $w = 1$ 运行，表示 Detje 的第一次行走。她从左边开始一个一个地经过鸟，并可能改变它们的状态。样例程序在看到第 $(i + 1)$ 只鸟之前，必须输出第 $i$ 只鸟的状态。 Detje 到达学校后，鸟的状态如下所示：  在程序的最后一次运行（$w = 2$）中，Detje 从学校回家。记住，在这种情况下，她会从右向左经过鸟，并按这个顺序处理它们！这意味着她需要在看到第 $(i - 1)$ 只鸟之前确定第 $i$ 只鸟的状态。 她完成行走后，鸟现在看起来如下所示：  确实，这是正确的配置。例如，鸟雕像 $3$（即从左数第四个）是打开的（现在 $b_3 = 1$），这正确的，因为人 $4$ 将搬到那里（$a_3 = 4$），并且他们原本有一个打开的鸟雕像（原本 $b_4 = 1$）。 --- **数据范围** 对于全部数据，$2\le N\le 500$，你至多使用 $W\le 60$ 轮。 - 子任务一（至多 $10$ 分）：$N=2$。 - 子任务二（至多 $24$ 分）：$N\le 15$。 - 子任务三（至多 $9$ 分）：$a_i=N-1-i$。 - 子任务四（至多 $13$ 分）：$a_i=(i+1)\bmod N$。 - 子任务五（至多 $13$ 分）：$a_i=(i-1)\bmod N$。 - 子任务六（至多 $31$ 分）：无特殊限制。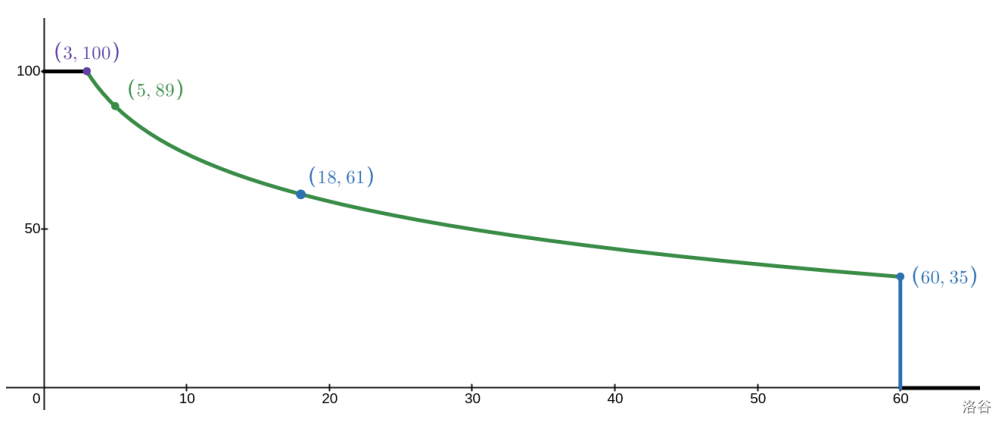 --- **评分方式** 对于每个你的程序正确解决的子任务，你会根据以下公式获得分数： $$ \textrm{score}=S_g\cdot\left(1-\frac{1}{2}\log_{10}(\max(W_g,3)/3)\right) $$ 其中 $S_g$ 是这个子任务的满分，$W_g$ 是你的程序在这个子任务的所有测试点中使用的最大轮数。你每个子任务的得分将被取整到最接近的整数。 下面是得分关于 $W_g$ 的函数图象。要想得到满分，你需要用不超过 $3$ 轮解决每个测试点。