P10848 [EGOI 2024] Circle Passing / 传球游戏

Day 2 Problem A. 题面译自 [EGOI2024 circlepassing](https://wiki.egoi2024.nl/tasks/circlepassing/statement-isc.pdf)。翻译来自于 [ChatGPT](https://chatgpt.com/) 并进行人工校对，若有误请联系 [rui_er](https://www.luogu.com.cn/user/122461)。

这是 Anouk 高中的第一天；作为热身活动，她的体育老师让班级玩记忆名字的游戏。班上有 $2N$ 名学生。他们中的大多数人彼此不认识，但有 $M$ 对最好的朋友，他们一起做任何事情。每个学生最多有一个最好的朋友。 老师把所有学生安排成一个圆圈，连续给每个学生分配一个从 $0$ 到 $2N - 1$ 的编号。更具体地，对于每个 $0 \le i < 2N - 1$，学生 $i$ 和 $i + 1$ 站在一起。此外，学生 $0$ 和 $2N - 1$ 也站在一起。 由于老师希望每个人都能结识新同学，所以最好的朋友必须尽可能远离彼此，即相对而站。也就是说，形成第 $i$ 对好朋友的学生分别站在位置 $k_i$ 和 $k_i + N$，其中 $0 \le k_i < N$。 老师选择了两个学生 $x$ 和 $y$ 并将一个球交给学生 $x$。目标是将球传给学生 $y$，但每个学生只能将球传给另一个他们已经知道名字的学生。当然，最好的朋友彼此知道对方的名字。在老师解释规则期间，每个学生都认识了直接站在他们旁边的两个学生的名字。除此之外，没有人知道其他人的名字。 游戏玩了 $Q$ 次；每次老师选择两个学生。由于学生们没有注意，他们在游戏过程中不会学到任何新名字。在每场游戏中，从学生 $x$ 到学生 $y$ 需要的最少传球次数是多少？

输入的第一行包含三个整数，$N, M$ 和 $Q$，其中 $2N$ 是 Anouk 班上的学生数，$M$ 是最好朋友的对数，$Q$ 是进行的游戏次数。 第二行包含 $M$ 个整数 $k_0 ,\cdots, k_{M-1}$，其中 $k_i$ 描述了第 $i$ 对好朋友。对于每个 $i$，最好朋友分别站在位置 $k$ 和 $k + N$。每个学生最多有一个最好的朋友。 接下来的 $Q$ 行每行包含两个整数，$x_i$ 和 $y_i$，即第 $i$ 场游戏中选择的两个学生。

输出 $Q$ 行，第 $i$ 行包含一个整数，即第 $i$ 场游戏中所需的最少传球次数。

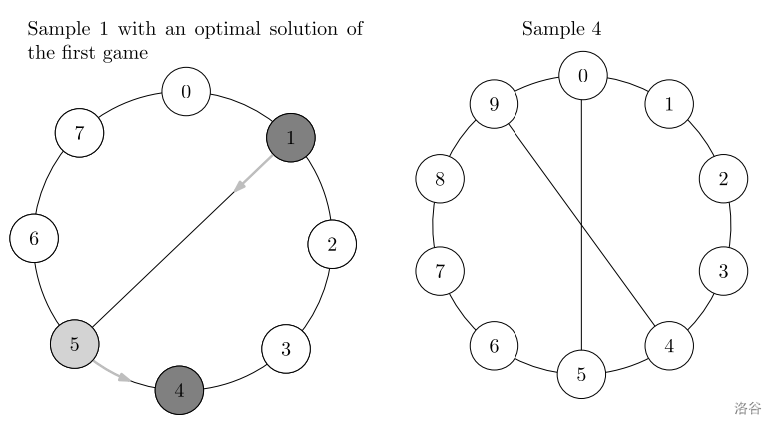
**样例解释** 以下两图描述了第一个样例和第四个样例中的排列情况。如果两个学生彼此认识，他们之间就有一条边连接。  在第一个样例的第一个游戏中，球被传给学生 $1$。学生 $1$ 将球传给他们的好朋友学生 $5$。球在学生 $5$ 传给学生 $4$ 后到达学生 $4$，总共需要两次传球。 --- **数据范围** 对于全部数据，$2\le N\le 5\times 10^8$，$1\le M\le 5\times 10^5$ 且 $M\le N$，$1\le Q\le 2\times 10^4$，$0\le k_0