P1096 [NOIP 2007 Junior] Hanoi Double Tower Problem

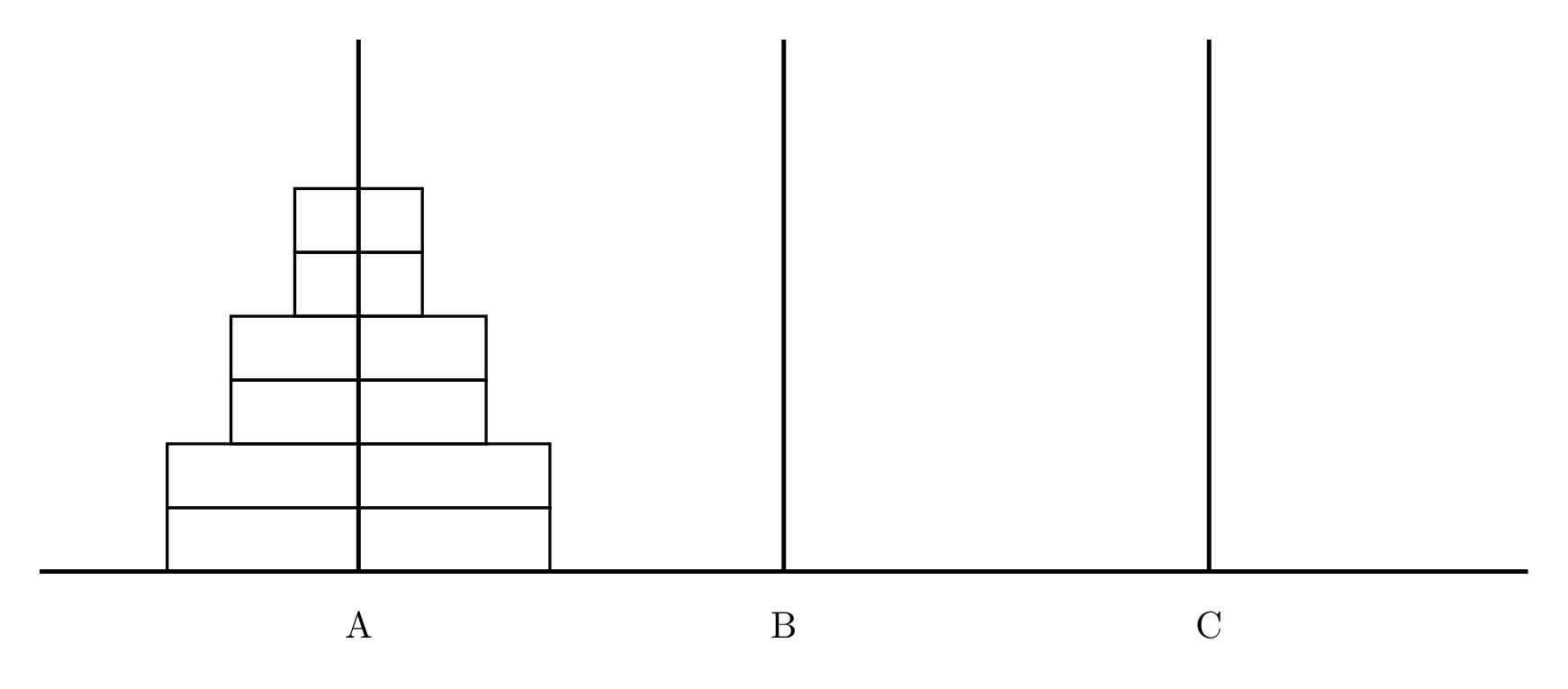
Given three sufficiently long thin pegs A, B, and C, there are $2n$ disks with holes on peg A. There are $n$ distinct sizes, and for each size there are two identical disks; note that these two disks are indistinguishable (the figure below shows the case $n=3$).  We need to move all these disks to peg C, and disks may be temporarily placed on peg B during the process. Requirements: 1. Only one disk may be moved at a time. 2. On pegs A, B, and C, the disks must always keep the order of smaller on top and larger below. Task: Let $A_n$ be the minimum number of moves required to complete the task for $2n$ disks. For the given $n$, output $A_n$.

A positive integer $n$, indicating there are $2n$ disks on peg A.

A positive integer, which is the minimum number of moves $A_n$ required to complete the task.

Constraints - 对于 $50\%$ 的数据，$1 \le n \le 25$； - 对于 $100\%$ 的数据，$1 \le n \le 200$。 Hint Try to establish a recurrence relation between $A_n$ and $A_{n-1}$. Translated by ChatGPT 5