P10997 【MX-J3-T4】 Partition
题目背景
原题链接:。
题目描述
你有 $n$ 行 $m$ 列的一个矩阵,第 $i$ 行第 $j$ 列的格子(记作 $(i,j)$)上写有一个整数 $a_{i,j}$。
- 称 $(a,b)$ 在 $(c,d)$ 的**下方**,当且仅当 $b=d,a>c$,即**同一列中,行编号更大**。
- 称 $(a,b)$ 在 $(c,d)$ 的**上方**,当且仅当 $(c,d)$ 在 $(a,b)$ 的**下方**。
- 称 $(a,b)$ 在 $(c,d)$ 的**右边**,当且仅当 $a=c,b>d$,即**同一行中,列编号更大**。
- 称 $(a,b)$ 在 $(c,d)$ 的**左边**,当且仅当 $(c,d)$ 在 $(a,b)$ 的**右边**。
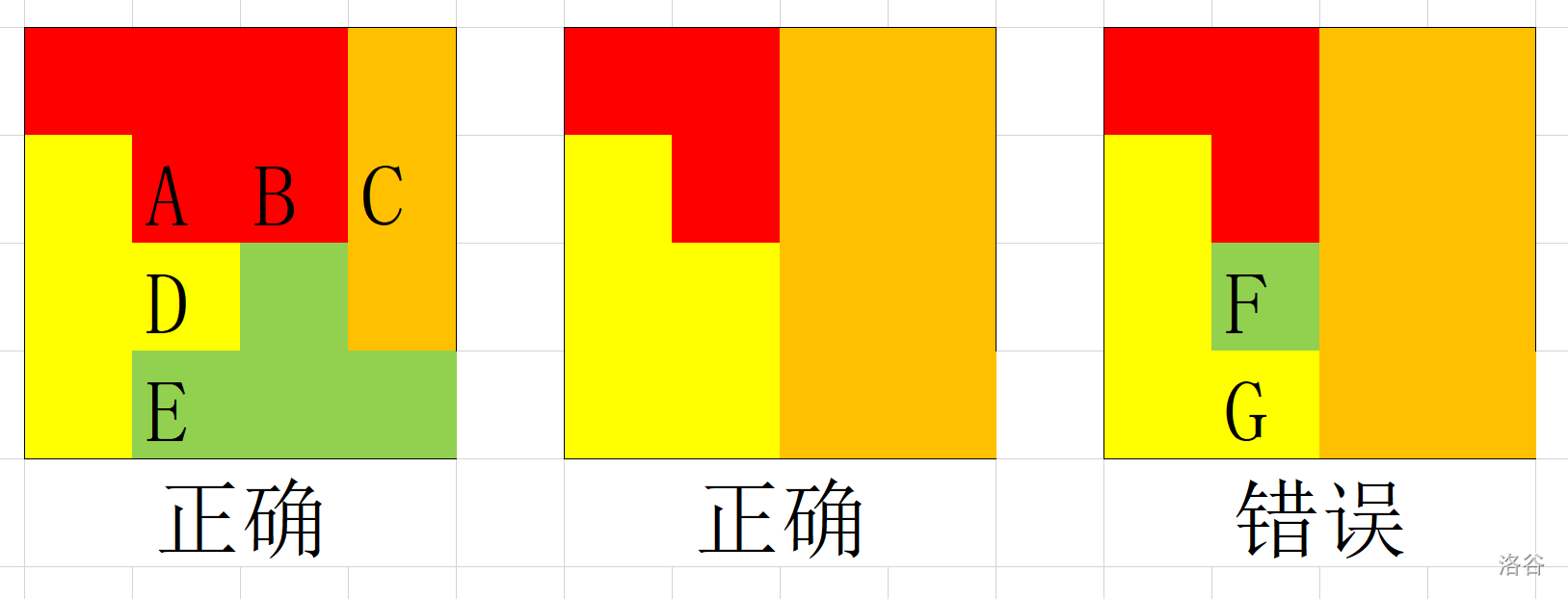
如图,$A(2,2)$ 下方有 $D(3,2),E(4,2)$,右边有 $B(2,3),C(2,4)$。
为了让矩阵更加美观,你想要给每个格子涂上红、橙、黄、绿四种颜色之一,有很多种方案,但是如果一个方案满足如下要求,就称这个方案是**简单**的:
- 红色格子的**上方**只能是红色格子,**左边**只能是红色或黄色格子,**右边**只能是红色或橙色格子。
- 橙色格子的**右边**只能是橙色格子,**上方**只能是橙色或红色格子,**下方**只能是橙色或绿色格子。
- 绿色格子的**下方**只能是绿色格子,**右边**只能是绿色或橙色格子,**左边**只能是绿色或黄色格子。
- 黄色格子的**左边**只能是黄色格子,**下方**只能是黄色或绿色格子,**上方**只能是黄色或红色格子。
上图中展示了一些可能的染色方案,其中:
- 第一幅图是简单的。
- 第二幅图也是简单的。注意如果一种颜色的格子不存在,那么可以直接忽略对应要求。
- 第三幅图不是简单的,因为 $F(3,2)$ 绿色格子下方有 $G(4,2)$ 是黄色,不符合第四条要求。
若 $(i,j)$ 的颜色为红、橙、黄、绿,则这个格子的权值 $w_{i,j}$ 分别为 $1,2,3,4$。计算所有简单的方案中,$\sum\limits_{i=1}^n\sum\limits_{j=1}^m a_{i,j} w_{i,j}$ 的最大值。
输入格式
输入的第一行是两个正整数 $n,m$,表示矩阵的行数和列数。
之后有 $n$ 行,每行 $m$ 个整数。第 $i$ 行第 $j$ 个整数表示 $a_{i,j}$。
输出格式
输出一行一个整数表示答案。
说明/提示
**【样例解释 #1】**

染色方案如上图所示。
**【数据范围】**
|测试点编号|$n,m\le$|特殊性质|
|:-:|:-:|:-:|
|$1\sim 3$|$4$||
|$4\sim 6$|$10$||
|$7\sim 11$|$500$||
|$12$|$2000$|$a_{i,j}\ge 0$|
|$13\sim 14$ |$1400$|$\vert a_{i,j}\vert \le 250$|
|$15\sim 20$|$2000$||
对于全体数据,保证 $1\le n,m\le 2000$,$|a_{i,j}|\le 10^9$。