P1099 [NOIP 2007 Senior] Core of the Treenetwork

Let $T=(V, E, W)$ be a connected undirected graph without cycles (also called an unrooted tree), where each edge has a nonnegative integer weight. We call $T$ a "treenetwork". Here $V$ and $E$ denote the sets of nodes and edges, respectively, $W$ denotes the set of edge lengths, and $T$ has $n$ nodes. Path: In a treenetwork, there is a unique simple path between any two nodes $a$ and $b$. Let $d(a, b)$ denote the length of the path whose endpoints are $a$ and $b$, i.e., the sum of the lengths of the edges on that path. We call $d(a, b)$ the distance between nodes $a$ and $b$. $D(v, P)=\min\{d(v, u)\}$, where $u$ ranges over the nodes on path $P$. Diameter of a treenetwork: The longest path in a treenetwork is called its diameter. For a given treenetwork $T$, the diameter is not necessarily unique, but it can be proved that the midpoint of any diameter (which may lie in the interior of an edge rather than exactly at a node) is unique; we call this point the center of the treenetwork. Eccentricity $\mathrm{ECC}(F)$: The distance from the farthest node in $T$ to path $F$, namely $$\mathrm{ECC}(F)=\max\{D(v, F), v \in V\}.$$ Task: Given a treenetwork $T=(V, E, W)$ and a nonnegative integer $s$, find a path $F$ which is a subpath on some diameter (the endpoints of this path are both nodes in the treenetwork), whose length does not exceed $s$ (it may equal $s$), such that the eccentricity $\mathrm{ECC}(F)$ is minimized. We call such a path the "Core" of treenetwork $T=(V, E, W)$. If necessary, $F$ may degenerate into a single node. In general, under the above definition, the core is not necessarily unique, but the minimal eccentricity is unique. 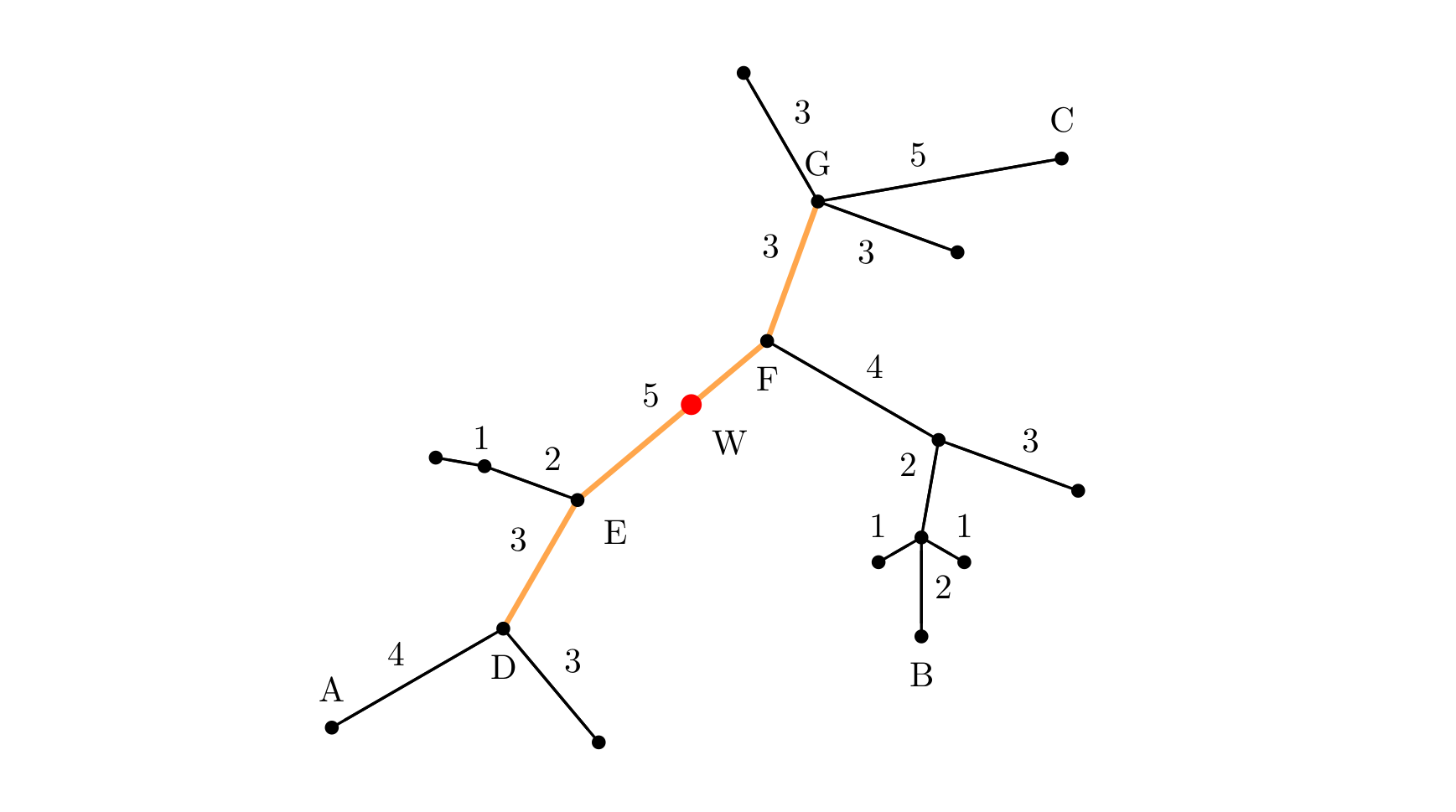The following figure gives an example of a treenetwork. In the figure, $A\!-\!B$ and $A\!-\!C$ are two diameters, both of length $20$. Point $W$ is the center of the treenetwork, and the length of edge $EF$ is $5$. If $s=11$ is specified, then the core of the treenetwork is path DEFG (it can also be taken as path DEF), and the eccentricity is $8$. If $s=0$ (or $s=1$, $s=2$), then the core of the treenetwork is node $F$, and the eccentricity is $12$. 

There are $n$ lines in total. Line $1$: two positive integers $n$ and $s$, separated by a single space. Here $n$ is the number of nodes in the treenetwork, and $s$ is the upper bound on the length of the core. The nodes are numbered $1, 2, \dots, n$. Lines $2$ through $n$: each line contains three space-separated integers $u, v, w$, indicating an edge between nodes $u$ and $v$ with length $w$. For example, `2 4 7` means the edge connecting nodes $2$ and $4$ has length $7$.

Output a single nonnegative integer: the minimal eccentricity under the given definition.

- For $40\%$ of the testdata, it is guaranteed that $n \le 15$. - For $70\%$ of the testdata, it is guaranteed that $n \le 80$. - For $100\%$ of the testdata, it is guaranteed that $2 \le n \le 300$, $0 \le s \le 10^3$, $1 \le u, v \le n$, $0 \le w \le 10^3$. NOIP 2007 Senior Problem 4. Translated by ChatGPT 5