P11023 [COTS 2020] 王国 Kraljevstvo

译自 [Izborne Pripreme 2020 (Croatian IOI/CEOI Team Selection)](https://hsin.hr/pripreme2020/) D1T1。$\texttt{1s,0.5G}$。

给定二维平面上的 $N$ 个点。选择 $K$ 个点，最大化这 $K$ 个点的凸包面积。 此外，要求必须选择平面上 $x$ 坐标最小/最大的两个点。保证这两个点所在的与 $y$ 轴平行的直线上没有其他点，且这两个点的 $y$ 坐标为 $0$。 只需要输出最大的面积。

第一行，两个正整数 $N,K$。 接下来 $N$ 行，每行两个整数 $x_i,y_i$，描述一个点。

输出一行一个实数，表示凸包的最大面积。 输出不应有多余的前导零或后导零。

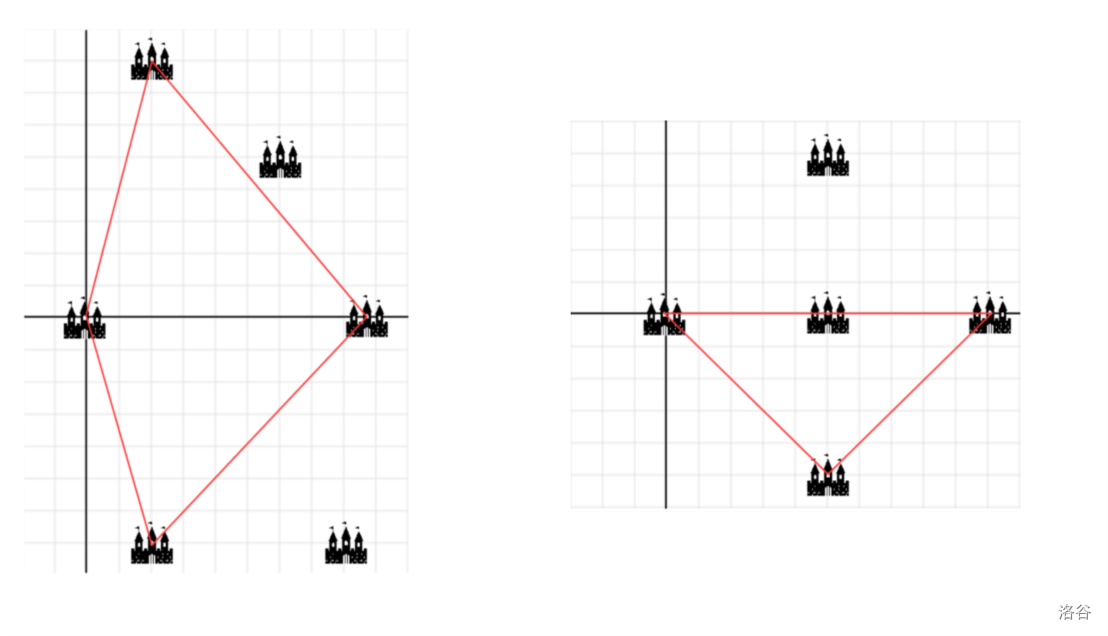
#### - 样例 $1$ 解释：选择 $(0, 0), (2, −7),(2, 8) , (9, 0) $ 即可。 - 样例 $2$ 解释：选择 $(0, 0), (10, 0) , (5, −5) $ 即可。 亦可参阅下图。  #### 数据范围 对于 $100\%$ 的数据，保证： - $3\le K\le N\le 3\, 000$； - $|x_i|,|y_i|\le 10^9$； - 给出的点不重合； - $x$ 坐标最小/最大的点唯一，且对应的点的 $y$ 坐标为 $0$。 | 子任务编号 | $N\le $ | 得分 | | :--: | :--: | :--: | | $ 1 $ | $20$ |$ 11 $ | | $ 2 $ | $100$ | $ 25 $ | | $ 3 $ | $500$ | $ 15 $ | | $ 4 $ | $3\, 000$ | $ 49 $ |