P11038 【MX-X3-T5】「RiOI-4」Countless J-Light Decomposition

原题链接：。 --- 「如果，如果，如果真的可以是那样的话，就好了啊。」 回想起自己做出的一个个选择，泠珞有时会想，自己是否有过更好的机会。 但是既然一切已经如此了，除了前进，别无他法。 无论结果是如何，接受结果，习得教训，然后……去争取更美好的未来。 那么，现在应该做的就是，尽可能避免，之后会走到的最坏结果了吧。 「规避风险。脚踏实地。做最可能实现的选择。」 「一定是的。」

给定一棵有根**带权**树，结点以 $1\sim n$ 编号。根结点编号为 $1$，边权均为正整数。 定义这棵树的**剖分**为对于每个结点，选择一些儿子（可以都选或都不选）为**重儿子**的方案。重儿子和其父亲的边称为**重边**。不是重边的边称为**轻边**。 定义一个剖分是 $\textbf{\textit{i--}}$**重的**，当且仅当对于每个结点，其重儿子数量不超过 $i$。 定义一个剖分是 $\textbf{\textit{j--}}$**轻的**，当且仅当对于每条从根（编号为 $1$ 的结点）出发的简单路径，其经过的轻边的边权和不超过 $j$。 对于 $i=0,1,\cdots,n-1$，请求出最小的 $j$，使得存在一个 $\textit{i--}$重的剖分是 $\textit{j--}$轻的。

无

无

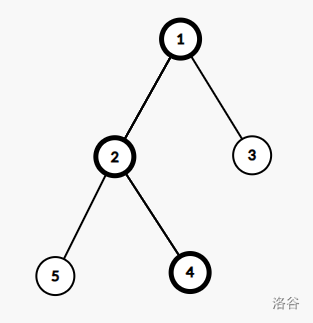
**【样例解释 #1】** 对于样例 1，其中的树如下所示：  当 $i=0$ 时，只存在一种剖分，不存在任何重儿子或重边。一条从根出发经过轻边边权和最大的简单路径为 $1\textit{---}2\textit{---}4$，边权和为 $2$。 当 $i=1$ 时，可以采用如图所示的剖分，加粗结点（根除外）为重儿子。一条从根出发经过轻边边权和最大的简单路径为 $1\textit{---}2\textit{---}5$，经过轻边的边权和为 $1$。 当 $i\ge 2$ 时，可以令所有的非根结点为重儿子，因此任何从根出发经过最多轻边的简单路径只能经过 $0$ 条轻边，故轻边最大边权和为 $0$。 **【样例解释 #2】** 当 $i\ge 3$ 时，可以令所有的非根结点为重儿子，因此任何从根出发经过最多轻边的简单路径只能经过 $0$ 条轻边，故轻边最大边权和为 $0$。 当 $i=0,1,2$ 时，我有一个很简洁的解释，但是这里空白太小写不下。 **【数据范围】** **本题开启捆绑测试。** |子任务|分数|$n\le$|特殊性质| |:-:|:-:|:-:|:-:| |$1$|$10$|$10^3$|| |$2$|$18$|$4\times10^4$|| |$3$|$16$|$10^5$|$w_i\le100$| |$4$|$21$|$10^5$|$w_i\le10^5$| |$5$|$35$|$2\times10^5$|| 对于 $100\%$ 的数据，$1\le n\le2\times10^5$，$1\le w_i\le 10^9$，保证输入是一棵树。