P11086 [ROI 2019] 机器人高尔夫 (Day 2)

翻译自 [ROI 2019 D2T3](https://neerc.ifmo.ru/school/archive/2018-2019/ru-olymp-roi-2019-day2.pdf)。 在“机器人奥林匹克运动会”中，有一个“机器人高尔夫比赛”。比赛场地是一个由 $n \times m$ 个单位方块组成的矩形。场地的行用数字 $1$ 到 $n$ 编号，列用数字 $1$ 到 $m$ 编号。每个单位方块由两个正整数 $r$ 和 $c$ 表示，分别代表它所在的行和列的编号。 两个机器人轮流在场地上移动一个特殊的“高尔夫球”，场地的某些方块上可能有洞。如果“高尔夫球”位于方块 $(r, c)$ 上，执行当前操作的机器人可以将其移动到方块 $(r + 1, c)$ 或方块 $(r, c + 1)$。如果“高尔夫球”位于最后一行或最后一列，机器人可以将其移动到场地的边界外。游戏会在以下两种情况下结束：“高尔夫球”超出了场地的边界，或者“高尔夫球”落到一个洞里。 每个洞对应一个整数 $v_i$，表示它的价值。游戏的结果等于游戏结束时“高尔夫球”所在洞的价值，如果“高尔夫球”超出了场地的边界，则结果为 $0$。先手机器人的目标是最小化游戏结果，而后手机器人的目标是最大化游戏结果。

假设 $g(r, c)$ 表示当“高尔夫球”初始位于方块 $(r, c)$ 时，先手机器人不论对手怎么行动都可以达到的最小游戏结果。由于比赛开始前不知道初始方块，机器人开发者想要计算出所有格子对应的 $g(r, c)$ 的总和，即 $\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}g(i,j)$。

第一行包含三个整数 $n,m,k$，分别表示行数、列数和洞的个数。 接下来的 $k$ 行，每行包含三个整数 $r_i,c_i,v_i$，分别表示洞所在的行、列编号和洞的价值。没有两个洞会位于同一个方块上。

输出一个整数，表示 $\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}g(i,j)\bmod998244353$。注意：输出的结果应该在 $0$ 和 $998244352$ 之间，而不是在 $-998244352$ 和 $998244352$ 之间。

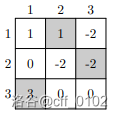
### 样例解释： 第一个样例中，所有方格的 $g(r,c)$ 如下（灰色的格子有洞）：  总结果求和为：$1 + 1 - 2 + 0 - 2 - 2 + 3 + 0 + 0 = -1$。答案为 $(-1) \bmod 998 244 353 = (-1 + 998 244 353) = 998 244 352$。 第二个样例中，所有方格的 $g(r,c)$ 如下：  总结果求和为：$1 + 2 + 0 - 3 + 1 + 0 - 3 - 3 = -5$。答案为 $(-5) \bmod 998 244 353 = 998 244 348$。 ### 数据范围： | 子任务 | 分值 | $n,m,k$ | 其它特殊性质 | | :----------: | :----------: | :----------: | :----------: | | $1$ | $20$ | $n,m\le1000$ | | | $2$ | $14$ | $n\le5,m\le10^9$ | | | $3$ | $14$ | $n,m\le100000,k=n+m-1$ | A | | $4$ | $10$ | | B | | $5$ | $6$ | $n,m\le100000$ | C | | $6$ | $6$ | | C | | $7$ | $10$ | $n,m\le100000$ | | | $8$ | $10$ | $k\le1000$ | | | $9$ | $10$ | | | 特殊性质 A：对于任意 $i$，$r_i=n$ 或 $c_i=m$。 特殊性质 B：对于任意 $i$，$r_i\ge n-1000$ 且 $c_i\ge m-1000$。 特殊性质 C：对于任意 $i$，$v_i=1$。 对于 $100\%$ 的数据，$1\le n,m\le10^9,1\le k\le\min(n\times m,10^5),1\le r_i\le n,1\le c_i\le m,|v_i|\le10^9$。