P11087 [ROI 2019] 考古 (Day 2)

翻译自 [ROI 2019 D2T4](https://neerc.ifmo.ru/school/archive/2018-2019/ru-olymp-roi-2019-day2.pdf)。 三〇一九年，在对古城市 Innopolis 进行挖掘时，考古学家发现了一件古代遗物——一个硬盘，里面存有一个文件，据推测，该文件包含了所有 ROI 题目的文本。 经过对文件的研究，发现其中的信息被编码成了一个由英文字母组成的字符串 $t$。题目文本相当长，并且包含了许多重复的内容，因此文件以压缩形式存储在硬盘上。解压缩文件使用以下算法： 在解压缩过程中，将生成一个由小写英文字母组成的字符串 $t$。初始时，字符串 $t$ 为空。压缩文件包含 $n$ 个块，必须按顺序处理每个块。每个块具有两种类型之一。 - 块 `1 w`，其中 $w$ 是一个字符串。处理此类块时，在字符串 $t$ 的末尾添加字符串 $w$。 - 块 `2 pos len`，其中 $pos$ 和 $len$ 是正整数。假设字符串 $t$ 中的字符从 $1$ 开始编号。处理此类块时，将字符串 $t$ 中从位置 $pos$ 开始的 $len$ 个连续字符依次添加到字符串 $t$ 的末尾。如果 $len$ 的值足够大，刚刚添加的一些字符可能会在处理同一块时再次使用。

考古学家们决定统计一个算法在 ROI 中考察的次数。为此，他们构建了一个由小写英文字母组成的字符串 $p$，并希望找出这个字符串在解压缩后的字符串 $t$ 中的出现次数。 如果长度为 $m$ 的字符串 $p$ 作为子串从位置 $i$ 开始出现，那么从第 $i$ 个字符开始的连续 $m$ 个字符串将是字符串 $p$。例如，字符串 `aba` 在字符串 `ababaaba` 中作为子串出现三次，分别从第 $1,3,6$ 个字符开始。 请编写一个程序，确定给定字符串 $p$ 在解压缩后的字符串 $t$ 中出现的次数。

第一行包含两个自然数 $m$ 和 $n$，分别表示字符串 $p$ 的长度和压缩文本中的块数。 第二行包含一个非空字符串 $p$，由小写英文字母组成。 接下来的 $n$ 行，包含按照题目背景的格式给出的块的描述。

输出一个整数，表示字符串 $p$ 在文本中出现的次数。

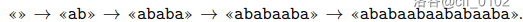
### 样例解释： $t$ 的解压缩过程是这样的：  `aba` 在 `ababaabaababaaba` 中出现了 $6$ 次。 ### 数据范围： 设将前 $i$ 块解压缩后字符串的长度为 $L_i$，第 $i$ 块的类型为 $type_i$。 | 子任务 | 分值 | $m\le$ | $n\le$ | $L_n\le$ | 其它特殊性质 | | :----------: | :----------: | :----------: | :----------: | :----------: | :----------: | | $1$ | $6$ | $2000$ | $1$ | $1000$ | | | $2$ | $10$ | $10^5$ | $2000$ | $10^6$ | | | $3$ | $10$ | $2000$ | $2000$ | $10^{10}$ | $\forall i>1,type_i=2,pos_i=1,L_1\mid len_i$ | | $4$ | $10$ | $2000$ | $2000$ | $10^{10}$ | $pos_i=L_{i-1}$ | | $5$ | $10$ | $20$ | $2000$ | $10^{10}$ | $pos_i=1,len_i\le10^7$ | | $6$ | $4$ | $2000$ | $2000$ | $10^{10}$ | $pos_i=1,len_i\le10^7$ | | $7$ | $10$ | $20$ | $20$ | $10^{10}$ | $p$ 只含字母 `a`，$pos_i+len_i-1\le L_{i-1}$ | | $8$ | $6$ | $20$ | $20$ | $10^{10}$ | $pos_i+len_i-1\le L_{i-1}$ | | $9$ | $2$ | $1$ | $2000$ | $10^{10}$ | $p$ 只含字母 `a` | | $10$ | $4$ | $20$ | $2000$ | $10^{10}$ | $p$ 只含字母 `a` | | $11$ | $5$ | $20$ | $2000$ | $10^{10}$ | | | $12$ | $14$ | $10^5$ | $2000$ | $10^{10}$ | | | $13$ | $9$ | $2\times10^5$ | $10000$ | $10^{15}$ | | 对于 $100\%$ 的数据，$\sum w\leq 2\times 10^5$。