P11090 [ROI 2021] 间谍游戏（IO 交互 + 通信题，暂无数据） (Day 1)

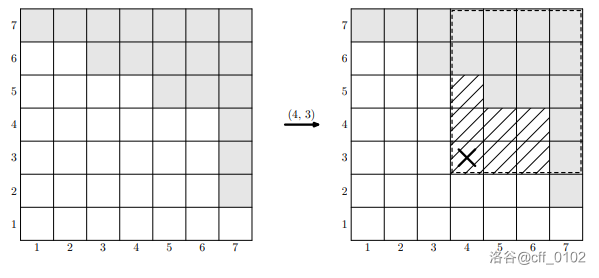
翻译自 [ROI 2021 D1T3](https://neerc.ifmo.ru/school/archive/2020-2021/ru-olymp-roi-2021-day1.pdf)。 **这是一道 IO 交互 + 通信题**。 一名间谍获得了一条重要消息，他需要将其传递给中心。由于消息十分重要，间谍决定将传递的消息伪装成一个正在流行的游戏。 这款游戏的规则非常简单。在一个大小为 $n\times n$ 的方形场地上，最初没有任何方格被涂色。两名玩家轮流进行行动。在一次行动中，玩家可以选择任何尚未填色的方格，并将从该方格左下角到整个方形场地的右上角所围成的矩形内的所有未填色方格都填色（见下图）。将方形场地左下角填色的玩家将输掉游戏。  间谍将在一个提供与 AI 对战的网站上进行游戏。AI 的行动方式如下：每次 AI 都以等概率随机选择一种行动，这些行动最多将 $k$ 个新方格涂上颜色（随机范围不包括左下角）。当然，如果左下角是唯一可行的选择，AI 将选择涂上这个方格并输掉游戏。 间谍可以玩任意数量的游戏，但为了隐藏身份，最好尽量少玩游戏。此外，为了显得更加自然，最好赢得尽可能多的游戏。通过记录所有已玩游戏中的行动，间谍要传递一个重要消息。 需要编写一个程序，它将被运行两次（解决两个任务）。在第一次运行时（在第一个任务中），该程序将扮演间谍的角色，与 AI 玩几局游戏，并同时传递秘密信息。在第二次运行时（在第二个任务中），只给出这些游戏的行动列表，程序需要还原出秘密信息。

在输入数据的第一行中，输入一个数字 $1$ 或 $2$，表示运行的次数（任务的编号）。 无论是第一次还是第二次运行，在第二行中都会输入三个数字：$n$，即方形场地的大小（在所有测试点中，$n = 32$），$k$，即机器人可以涂色的最大方格数（在所有测试点中，$k = 8$），$m$，即秘密信息的长度（以字符为单位）（除了样例外，所有测试点中 $m = 100000$）。 ### 在第一个任务中： 第三行包含那个秘密消息，也就是一个长度为 $m$ 的字符串，由字符 `0` 和 `1` 组成。在读取完它之后，你的程序应该开始与实现 AI 策略的交互库进行交互，与它交替进行行动。每一步用一对数字表示，即所选单元格的列和行号。列从左到右从 $1$ 到 $n$ 编号，行从下到上从 $1$ 到 $n$ 编号（见题目背景中的图片）。所选择的单元格不能是已经被涂色过的，否则交互将被中断，这个测试点的结果将变成 WA。当其中一位玩家做出操作 `1 1` 时，游戏结束，然后立即开始下一轮。在第一轮游戏中，程序是先手，在第二轮中，程序将变成后手，以此类推。 新的一轮开始时，如果你的程序认为这么多的游戏次数足以传递长度为 $m$ 的信息，不需要继续做出行动，而是输出一个数字 $0$，终止这次交互。如果此时 AI 是先手，它的第一个移动将不会记录在第二次运行的日志中。你不能在游戏中途停止交互。 如果在第一次运行时程序遵循规则进行了一定数量的游戏，并且符合时间和内存限制，则它将再次进行第二次运行。否则，不会进行第二次运行，并且第一次运行的结果（`WA`，`RE`，`TLE`，`MLE` 或 `OLE`）将成为测试点的结果。 ### 在第二个任务中： 第三行包含在第一次运行中玩过的游戏数量。然后会按照游戏进行的顺序输入在所有游戏中所做的移动列表，包括你的程序和交互库的移动。在第二次运行中，程序需要应输出一个长度为 $m$ 的字符串，由 `0` 和 `1` 组成，表示秘密消息。 你需要先从标准输入读取**所有数据**，然后再输出答案。 如果第二次运行的结果是 `RE`，`TLE`，`MLE` 或 `OLE`，则该结果将成为该测试点的结果。否则，将检查程序输出的答案。如果它与第一次运行传递给程序的秘密消息相匹配，则测试结果将是 `AC`，否则为 `WA`。

在每个输出之后，请输出换行符并刷新输出流。 如果在 C++ 中使用了 `cout

上面的样例仅用于了解输入和输出的格式。特别要注意的是，在所给的样例中，间谍实际上不一定通过某种方式在给定的步骤序列中传递了任何信息。 在示例中，输入和输出之间通过空行进行了格式化。在实际交互中，应在每个查询后加换行符，但无需输出空行。 程序将在 $10$ 个测试点中运行，每个测试点最多可以获得 $10$ 分。 每个测试点中有一个秘密消息，并且长度为 $m = 100,000$。在每个测试点中，消息是由随机数生成器生成的，每个字符以相等的概率独立地选为 `0` 或 `1`。 交互库在每个测试中采取的动作是随机的，符合题目中的描述。但是，在重复运行时，如果参赛程序做出相同的动作，交互程序也会在该测试中做出相同的动作。 如果程序在第二次运行时无法正确恢复消息，或者在第一次运行时违反了规定，则该测试将获得 $0$ 分。 否则，测试点得分取决于第一次运行时玩的游戏数量和赢得的游戏数量。 设 $W$ 为你是否输掉不超过一场比赛（如果输掉超过一场比赛，则 $W = 0$，否则 $W=1$），$G$ 为玩的游戏数量，$B = \frac{m} {G}$ 为每次游戏平均传达几位秘密消息。数字 $b_i$ 表示获得 $i$ 分所需的值 $B$，并在下表中给出。  如果 $B > b_9$，则你将获得 $W + 9$ 分。否则，设 $s$ 是满足 $b_s \le B < b_{s+1}$ 的值，在这种情况下，你将获得 $W +s+ \frac{B−b_s} {b_{s+1}−b_s}$ 分。单个测试的分数将累加，并且最终总分将四舍五入为最接近的整数。 本题暂无数据。一种可能在洛谷实现这种通信的方法是：任务一用 IO 交互，任务二直接调用函数（但可能还需要加防作弊）。本题的数据文件已经放在附件（其中的输入输出数据已经手动改为 `.in` 和 `,out` 文件），可以自行测试，也欢迎提供交互库。