P11092 [ROI 2021] 莫斯科数字 (Day 2)

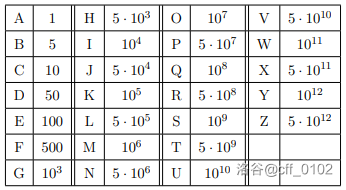
翻译自 [ROI 2021 D2T1](https://neerc.ifmo.ru/school/archive/2020-2021/ru-olymp-roi-2021-day2.pdf)。 你可能熟悉罗马数字，并且也听说过莫斯科是第三个罗马的说法，所以我们隆重推出莫斯科数字。这是罗马数字的进阶版本，与之类似。在莫斯科数字系统中，数字由大写英文字母 `A` 到 `Z` 表示。每个数字对应一个特定的值：  莫斯科数字规则如下：每个数字的值等于由它构成的各个数字的总和。数字可以有正负之分。如果一个数字右侧没有比它更大的数字，则该数字的值等于它本身；否则，该数字的值等于其本身取负。例如： - 「`BBA`」的值为 $5 + 5 + 1 = 11$； - 「`BBBC`」的值为 $-5 + (-5) + (-5) + 10 = -5$； - 「`ABC`」的值为 $-1 + (-5) + 10 = 4$； - 「`BAC`」的值为 $-5 + (-1) + 10 = 4$； - 「`ACA`」的值为 $-1 + 10 + 1 = 10$； - 「`CFF`」的值为 $-10 + 500 + 500 = 990$。 给定了一些数字，每个数字由大写英文字母组成（即莫斯科数字），但是一部分被替换成了问号。对于每个数字，需要确定在将问号替换为莫斯科数字字母后，可以得到的最大数字。

第一行是一个整数 $t$，表示数据组数，即数字的数量（$1 \le t \le 50000$）。 接下来的 $t$ 行，每行一个字符串 $s_i$，由大写英文字母和问号组成。所有字符串的长度之和不超过 $300000$。

对于每个输入，输出两行，都表示的是将问号替换为莫斯科数字字母后可以得到的最大数字。第一行是以十进制表示的最大数字值，第二行就是替换后的这个最大莫斯科数字。

设 $S=\sum\limits^{t}_{i=1}|s_i|$。 | 子任务 | 分值 | $S\le$ | 特殊性质 | | :----------: | :----------: | :----------: | :----------: | | $1$ | $6$ | $1000$ | $s_i$ 中不包含 `?` | | $2$ | $9$ | $3\times10^5$ | $s_i$ 中不包含 `?` | | $3$ | $40$ | $1000$ | $s_i$ 中不包含超过三个 `?` | | $4$ | $20$ | $1000$ | | | $5$ | $25$ | $3\times10^5$ | |