P11094 [ROI 2021] 砍树 (Day 2)

翻译自 [ROI 2021 D2T3](https://neerc.ifmo.ru/school/archive/2020-2021/ru-olymp-roi-2021-day2.pdf)。 “2D” 组织负责发放伐木许可证。他们收到了沿公路的伐木申请。 公路上有 $n$ 棵树，其中第 $i$ 棵树生长在坐标为 $x_i$ 的点上，高度为 $h_i$。关于这些树的信息被排序，满足 $x_1 < x_2 < \dots < x_{n-1} < x_n$。 可以按以下方式逐个砍伐树木：将树砍倒，并让它向左或向右倒下。为了防止树木在倒下时受损，它不应碰到距离它自身高度以内的未砍伐的树木。换句话说，如果位于坐标为 $x_i$，高度为 $h_i$ 的树木向右倒下，则不应该存在坐标为 $x_j$ 的未砍伐的树木，使得 $x_i < x_j < x_i + h_i$。如果同一树木向左倒下，则不应存在坐标为 $x_j$ 的未砍伐的树木，使得 $x_i − h_i < x_j < x_i$。 左边界 $x_1$ 处的树木和右边界 $x_n$ 处的树木旁边有重要的建筑物，因此不允许倒掉的树木落在区间 $[x_1, x_n]$ 之外。换句话说，如果 $x_i − h_i < x_1$，坐标为 $x_i$，高度为 $h_i$ 的树木不能向左倒下；如果 $x_i + h_i > x_n$，坐标为 $x_i$，高度为 $h_i$ 的树木不能向右倒下。 组织收到了 $q$ 个伐木申请。每个申请由两个数字 $l_i$ 和 $r_i$ 组成，表示申请者希望砍伐第 $l_i$ 到第 $r_i$ 个树木（包括边界）。 在执行申请的过程中，只允许砍伐从 $l_i$ 到 $r_i$ 编号的树木。被砍伐的树木可以倒到 $l_i$ 的左边或 $r_i$ 的右边的区域，但不能超出 $[x_1, x_n]$ 范围，也不允许触碰 $l_i$ 到 $r_i$ 范围之外的其它树木。 对于每个申请，需要计算在不损坏任何树木的情况下可以砍倒的最大树木数量。每个申请都应独立处理（只是申请了，树没有真的被砍掉）。

第一行包含两个整数 $n$ 和 $q$。 接下来的 $n$ 行描述每棵树，每行包含两个整数 $x_i$ 和 $h_i$。保证 $x_1 < x_2 < \dots < x_n$。 然后是 $q$ 个伐木申请的描述，每个申请占一行。第i行包含两个整数 $l_i$ 和 $r_i$。

对于每个申请，输出可以砍伐的最大树木数量。

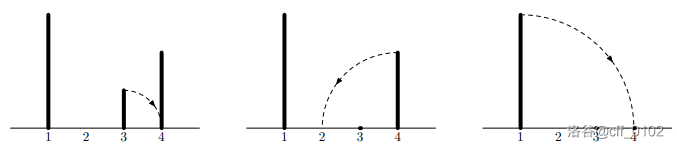
样例一最后一个询问可以这样砍：  对于 $100\%$ 的数据，$1 \le n, q \le 500000,1 \le x_i, h_i \le 10^9,1 \le l_i \le r_i \le n$。 | 子任务 | 分值 | $n,q\le$ | | :----------: | :----------: | :----------: | | $1$ | $15$ | $100$ | | $2$ | $15$ | $500$ | | $3$ | $15$ | $5000$ | | $4$ | $5$ | $10000$ | | $5$ | $10$ | $100000$ | | $6$ | $10$ | $200000$ | | $7$ | $30$ | $500000$ |