P11104 [ROI 2023] 监控 (Day 1)
题目背景
翻译自 [ROI 2023 D1T1](https://neerc.ifmo.ru/school/archive/2022-2023/ru-olymp-roi-2023-day1.pdf)。
商场大楼的安全由视频监控系统提供保障。
安保人员的电脑上有一个程序,该程序在屏幕上显示出多个摄像头的视频。该程序的工作原理如下:
屏幕上显示一个由 $h$ 行 $w$ 列组成的矩形网格。每个单元格可以为空,也可以显示来自某个摄像头的图像。为了控制程序中图像的位置,安保人员可以使用“左”、“右”、“上”和“下”按钮。
- 按下“左”按钮会将每个单元格中的图像向左移动到其左边的单元格。最左边一行的图像会被移动到最右边一行的对应单元格中。
- 按下“右”按钮会将每个单元格中的图像向右移动到其右边的单元格。最右边一行的图像会被移动到最左边一行的对应单元格中。
- 按下“上”按钮会将每个单元格中的图像向上移动到其上方的单元格。最上面一行的图像会被移动到最下面一行的对应单元格中。
- 按下“下”按钮会将每个单元格中的图像向下移动到其下方的单元格。最下面一行的图像会被移动到最上面一行的对应单元格中。
网格的行由上至下编号,列由左至右编号。$(r, c)$ 表示第 $r$ 行第 $c$ 列的单元格。
下面是一个有 $3$ 行 $4$ 列和三个包含图像的单元格的网格示例,其坐标分别为 $(1, 1),(2, 4),(3, 3)$,还显示了按下四个按钮后图像的新位置。
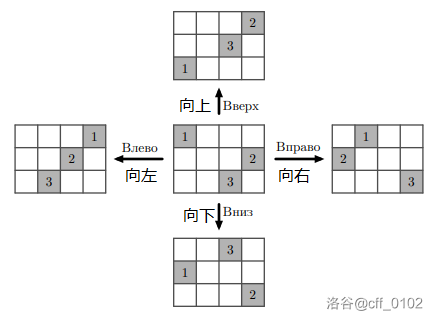
题目描述
安保人员希望屏幕上显示图像的单元格尽可能紧凑。图像的紧凑性可以用网格中包含所有显示的图像所需的最小矩形的面积来衡量。通过按下按钮可以改变图像的紧凑性。例如,下图刚开始的图像布局紧凑性为 $12$,按下一次“右”按钮和一次“上”按钮后,图像的紧凑性变为 $4$。
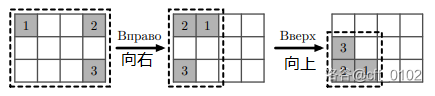
给定一个包含 $k$ 个图像的网格,计算通过使用“左”、“右”、“上”和“下”按钮可以达到的最小紧凑性,并计算达到最小紧凑性所需的最小按钮点击次数。
输入格式
第一行输入三个整数 $h,w,k$,分别表示网格的尺寸和包含图像的单元格数量($1 \le h, w \le 10^9;1 \le k \le 100,000$)。
接下来的 $k$ 行中,每行包含两个整数 $r_i$ 和 $c_i$,表示包含图像的单元格的坐标($1 \le r_i \le h;1 \le c_i \le w$)。保证所有 $k$ 个单元格坐标均不相同。
输出格式
输出两个整数,分别表示使用按钮所能达到的最小图像紧凑性和实现该紧凑性所需的最小按钮点击次数。
说明/提示
| Subtask | 分数 | 特殊性质 |
| :----------: | :----------: | :----------: |
| $1$ | $5$ | $k=1$ |
| $2$ | $10$ | $k=2$ |
| $3$ | $29$ | $h=1$ |
| $4$ | $11$ | $h,w\le50$ |
| $5$ | $15$ | $h,w\le1000$ |
| $6$ | $6$ | $h,w\le200000$ |
| $7$ | $24$ | 无 |