P11108 [ROI 2023] 蜗牛与富士山 (Day 2)
题目背景
翻译自 [ROI 2023 D2T1](https://neerc.ifmo.ru/school/archive/2022-2023/ru-olymp-roi-2023-day2.pdf)。
在爬上富士山的山顶后,蜗牛想要下山。在山坡上有一个类似二叉树的小径。
该树包含 $n$ 个被 $n-1$ 个小径连接的节点。树的根位于山顶。一些节点处的小径到头了,它们是树的叶子节点。除了叶子节点外,每个节点向下山坡延伸两条小径,其中一条向左,另一条向右。
蜗牛希望从根部开始沿着树向下爬并到达其中一个叶子节点。在路径上,蜗牛可以选择两个方向之一进行进一步下降:向左或向右。
刚开始在山顶,蜗牛可以往任意方向(左或右)开始下降。在每个后续节点中,如果它选择与前一个节点选择的方向不同的方向,则它要进行转弯。
由于蜗牛转弯不太方便,所以在从根到叶子的整个路径上,蜗牛最多只准备转弯 $k$ 次。
题目描述
将树的节点从 $1$ 到 $n$ 编号,其中根节点编号为 $1$。给定 $q$ 个查询。每个查询给出一个节点 $u_i$,要求找出蜗牛在从根开始下降时,最多转弯 $k$ 次,且通过节点 $u_i$ 的路径上能到达的叶子节点数量。
输入格式
第一行给出三个整数 $n,k,q$,分别表示树中节点的数量、蜗牛准备转动的最大次数,以及查询的数量。
接下来的 $n$ 行描述了树的结构。第 $i$ 行的第一个整数 $t_i$ 表示节点 $i$ 的小径(子树)数量($t_i = 0$ 或 $2$)。如果 $t_i = 2$,则在同一行中给出两个整数 $l_i$ 和 $r_i$,分别表示从节点 $i$ 出发的左侧和右侧小径连接到的节点编号($1 \le l_i,r_i \le n$)。保证输入符合要求。
接下来的 $q$ 行给出了查询。第 $i$ 行给出一个整数 $u_i$,表示蜗牛路径经过的节点编号($1 \le u_i \le n$)。
输出格式
对于每一次询问,输出一行一个整数表示答案。
说明/提示
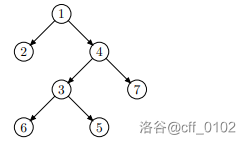
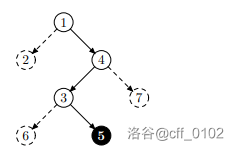
样例的树长这样。
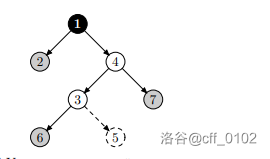
第一次询问(灰色为可到达的叶子节点,虚线为不可到达的节点):
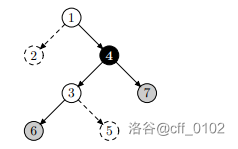
第二次询问:
第三次询问:
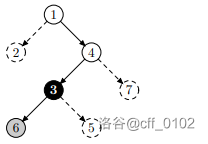
第四次询问(因为最多转一次弯,所以并没有合法的路线,故输出 $0$):
对于 $100\%$ 的数据,$3 \le n \le 200000$,$0 \le k \le n$,$1 \le q \le 200000$。
| Subtask | 分值 | 特殊性质 |
| :----------: | :----------: | :----------: |
| $1$ | $11$ | $n\le500,q\le500$,所有 $u_i$ 均为叶子节点 |
| $2$ | $12$ | $n\le500,q\le500$ |
| $3$ | $10$ | $k=n$ |
| $4$ | $14$ | $k=0$ |
| $5$ | $19$ | 所有 $u_i$ 均为叶子节点 |
| $6$ | $34$ | 无 |