P11113 [ROI 2024] 2026 (Day 1)

翻译自 [ROI 2024 D1T2](https://neerc.ifmo.ru/school/archive/2023-2024/ru-olymp-roi-2024-day1.pdf)。 一款新的游戏《2026》在一个 $m$ 行 $n$ 列的矩形盘面上进行。盘面被划分为 $m \times n$ 个 $1 \times 1$ 的小格子。在一些格子上放置了大小为 $1 \times 1$ 的方块，每个方块上写有一个英文字母。 你需要进行 $q$ 次操作，每次操作都是将所有方块向一个方向移动到底。因此，操作序列由一个长度为 $q$ 的字符串 $s$ 给出，字符串中每个字符表示一个方向：`L` 表示向左移，`R` 表示向右移，`U` 表示向上移，`D` 表示向下移。 具体操作与游戏《2048》相类似：在棋盘上，只要有一个方块在指定方向上相邻的格子是空的，该方块就会移动到该空格子上，包括它后面的那些方块也会连带着向那个方向一起移动，直到前方没有空格。

给出棋盘的初始状态和操作序列，请确定所有操作执行完成后盘面的状态。

输入包含多组数据。 - 第一行输入一个整数 $t$ ，表示测试数据的组数（$1 \le t \le 200 000$）。 - 对于每组数据： - 第一行输入整数 $m$ 和 $n$，代表盘面的大小（$1 \le m, n \le 10^6$，$1 \le m \times n \le 10^6$）。 - 接下来的 $m$ 行，输入盘面的初始状态： - 其中的第 $i$ 行（$1 \le i \le m$）包含一个长度为 $n$ 的字符串 $a_{i1}a_{i2}\dots a_{in}$，表示第 $i$ 行的盘面状态。 - 每个字符 $a_{ij}$ 要么是小写英文字母（从 `a` 到 `z`），要么是点号 `.`。如果 $a_{ij}$ 是 `.`，则表示第 $i$ 行第 $j$ 列的格子为空，否则表示该格子上有一个标有字母 $a_{ij}$ 的方块。 - 最后一行输入一个字符串 $s$，由 $q$ 个字符组成，表示操作的序列（$1 \le q \le 10^6$）。每个字符都是 `L`，`R`，`U`，`D` 之一。 所有测试数据中 $m \times n$ 的总和不超过 $2 \times 10^6$，$q$ 的总和不超过 $2 \times 10^6$。

对于每组数据，输出执行完所有操作后的盘面，格式与输入相同。

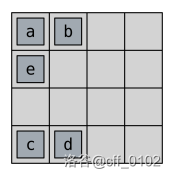
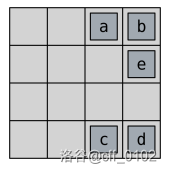
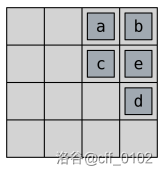
样例解释： 在第一组输入数据中，盘面最初看起来是这样的：  第一次操作将所有方块向左移动。接着，盘面会变成这样：  第二次操作将所有方块向右移动。接着，盘面会变成这样：  第三次，也是最后一次操作将所有方块向上移动。所有操作结束后，盘面会变成这样：  | 子任务 | 分值 | 特殊性质 | | :----------: | :----------: | :----------: | | $1$ | $9$ | $t=1,q=1,n,m\le100$ | | $2$ | $7$ | $s_i$ 只可能为 `L` 或 `R` | | $3$ | $13$ | $\sum mnq\le10^7$ | | $4$ | $14$ | $s_i$ 只可能为 `L` 或 `R` 或 `U` | | $5$ | $12$ | 棋盘上所有字母都是 `a`，$\sum mq\le10^7$ | | $6$ | $11$ | 棋盘上所有字母都是 `a` | | $7$ | $9$ | 棋盘初始状态是“阶梯状”的，具体地，第 $i$ 行仅最左侧恰有 $i-1$ 个字母 | | $8$ | $14$ | $s$ 是重复若干次的 `LURD` | | $9$ | $11$ | 无 |