P11117 [ROI 2024] 交互式通道 (Day 2)

翻译自 [ROI 2024 D2T2](https://neerc.ifmo.ru/school/archive/2023-2024/ru-olymp-roi-2024-day2.pdf)。 ROI 的举办地 Innopolis 大学由 $n$ 个建筑物和 $m$ 条通道组成。每条通道连接两个不同的建筑物，任何两个建筑物之间不会有多于一条通道。 已知每个建筑物都有一个可以打开或关闭的灯光。最初，所有建筑物的灯光都是关闭的。校园管理员可以在一个操作中打开或关闭任何一个建筑物的灯光。管理员还可以在灯光已经打开的情况下按下开灯按钮，或在灯光已经关闭的情况下按下关灯按钮。这些操作不会改变建筑物的灯光状态。 类似地，每条通道也有一个可以打开或关闭的灯光。最初，所有通道的灯光也都是关闭的。但与建筑物的灯光不同，通道的灯光会自动变化：如果在管理员的操作后，该通道连接的两所建筑物的灯光状态相同，那么通道的灯光也会变为相同的状态，否则它不会改变。 换句话说，如果在管理员的操作后，连接的两个建筑物的灯光都关闭，则通道的灯光也会关闭。如果连接的两个建筑物的灯光都打开，则通道的灯光也会打开。如果一个建筑物的灯光打开而另一个关闭，则通道的灯光状态不变。

在 ROI 开始之前，校园主任为每个建筑物和每条通道确定了它们是否应该被照亮。请你检查管理员是否可以通过任意数量的操作来实现主任的要求。如果可以，请找到任何一种满足要求的操作序列。能够正确判断是否可以得到期望的灯光状态，即使未提供操作序列的解决方案，也能获得该测试点一半的分数。

输入包含多组数据。第一行包含一个整数 $t$，表示测试数据的组数（$1 \leq t \leq 50000$）。 在每组数据中： 第一行输入两个整数 $n$ 和 $m$，分别表示建筑物的数量和通道的数量（$1 \leq n \leq 10^5$, $0 \leq m \leq 2 \times 10^5$）。 接下来的 $m$ 行是通道的描述。在第 $i$ 行中有三个整数 $a_i$, $b_i$, $c_i$ ，分别是由第 $i$ 个通道连接的两个建筑物编号，以及第 $i$ 个通道要求的灯光状态（$1 \leq a_i, b_i \leq n$, $a_i \ne b_i$, $0 \leq c_i \leq 1$）。如果 $c_i = 0$，则第 $i$ 个通道的灯光状态最终应该是关闭的，如果 $c_i = 1$，则应该是开启的。 最后一行给出 $n$ 个整数 $d_1, d_2, \dots, d_n$，表示各建筑物要求的灯光状态（$0 \leq d_i \leq 1$）。如果 $d_v = 0$，则建筑物 $v$ 的灯光状态最终应该是关闭的，如果 $d_v = 1$，则应该是开启的。 所有 $n$ 值的总和不超过 $10^5$，$m$ 值的总和不超过 $2 \times 10^5$。

对于每组输入： - 如果不存在一种操作序列能使得建筑物和通道的灯光状态达到要求，则输出 `NO`。 - 如果存在操作序列，则输出 `YES`。如果不展示具体的操作序列（只拿部分分），则在下一行输出数字 $-1$ 并继续输出下一组数据（如果有的话）。如果展示操作序列，则在下一行输出整数 $s$，表示操作的数量（$0 \leq s \leq 10^6$，所有 $s$ 值的总和不超过 $10^6$），然后在接下来的 $s$ 行中输出下列具体操作： - 在第 $i$ 行（$1 \leq i \leq s$）中，输出两个整数 $v_i,x_i$，分别是改变灯光状态的建筑物编号，以及新的灯光状态（$1 \leq v_i \leq n$，$0 \leq x_i \leq 1$；如果 $x_i = 0$，则表示需要关闭建筑物 $v_i$ 的灯光，如果 $x_i = 1$，则表示需要打开建筑物 $v_i$ 的灯光）。

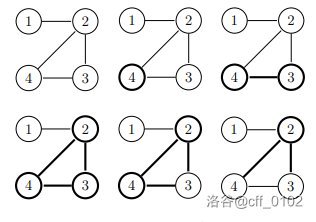
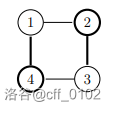
样例解释： 第一组数据包含 $4$ 个建筑物（用圆圈表示）和 $4$ 条通道（用线表示）。机房或通道的灯光状态通过加粗的线表示（如果加粗则表示开灯）。要达到所需的灯光状态，需要 $5$ 步操作。下图展示了初始灯光状态及每一步操作后的状态：  第二组数据需要达到下列机房和通道的配置，但这是不可能的：  第三组数据中有一个建筑物需要开启灯光。这可以通过一步操作完成。 第四组数据中有一个建筑物需要关闭灯光。一个可行的操作序列是一步操作，关闭该机房的灯光。尽管灯光已经是关闭状态，这样的操作依然是有效的。 第五组数据中有两个建筑物和一条通道，所有的灯光都需要关闭。空的操作序列也是一种可行的解决方案。 数据范围见输入格式。