P11127 [ROIR 2024] 二叉树的遍历 (Day 2)

翻译自 [ROIR 2024 D2T4](https://neerc.ifmo.ru/school/archive/2023-2024/ru-olymp-regional-2024-day2.pdf)。 二叉树有三种基本遍历方式：前序遍历（pre-order）、中序遍历（in-order）和后序遍历（post-order）。我们可以将这三种遍历方式进行概括：假设每个节点上记录一个整数 $x$（取值范围为 $-1$ 到 $1$），表示在遍历中输出该节点的时机，具体如下： - $x = -1$：在遍历其左右子树之前； - $x = 0$：在遍历其左子树之后，遍历其右子树之前； - $x = 1$：在遍历其左右子树之后。 因此，如果所有节点的 $x$ 值都是 $-1$，则遍历为前序遍历；如果都是 $0$，则为中序遍历；如果都是 $1$，则为后序遍历。

考虑一棵有 $n$ 个节点的二叉树，节点编号从 $1$ 到 $n$。树的根节点为 $1$。最初，所有节点上的值都是 $-1$。 你需要处理 $q$ 个操作，操作类型如下： 1. 将节点 $l, l + 1, \dots, r$ 上的值更改为 $x$（$x$ 取值为 $-1$，$0$ 或 $1$）。 2. 查询节点 $i$ 在当前遍历方式中的位置。 需要输出所有第二种类型的操作的结果。

第一行包含两个整数 $n$ 和 $q$（$1 \leq n, q \leq 100000$）。 接下来 $n$ 行，每行包含两个整数 $L_i$ 和 $R_i$（$0 \leq L_i, R_i \leq n$），分别表示节点 $i$ 的左子树和右子树的编号，若某个子树不存在则为 $0$。 保证 $L_i$ 和 $R_i$ 描述了一个有效的二叉树。 接下来的 $q$ 行中包含操作。每行的第一个整数 $t$（$t \in \{1, 2\}$）表示操作类型。 - 对于第一种类型的操作，后面有三个整数 $l$，$r$ 和 $x$（$1 \leq l \leq r \leq n$，$x$ 为 $-1$，$0$ 或 $1$），表示节点范围和新的值。 - 对于第二种类型的操作，后面有一个整数 $i$（$1 \leq i \leq n$），表示询问其在遍历中的位置的节点编号。

对于每个第二种类型的操作，输出一个整数，表示对应节点在遍历中的位置。

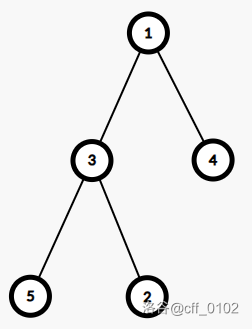
样例中的树是这样的：  刚开始，所有节点的 $x$ 值都是 $-1$，因此第一次查询时遍历得到的数组为 $[1,3,5,2,4]$，$2$ 在第四个位置。 在将节点 $1,2,3$ 的遍历方式 $x$ 改为 $1$ 后，再次查询时遍历得到的数组为 $[5,2,3,4,1]$，$5$ 在第一个位置。 接着把节点 $3$ 的遍历方式 $x$ 改为 $0$，此时再进行查询，遍历得到的数组为 $[5,3,2,4,1]$，$3$ 在第二个位置。 设 $q_1$ 为操作 $1$ 的数量。 | 子任务 | 分值 | 特殊性质 | | :----------: | :----------: | :----------: | | $0$ | $0$ | 同样例 | |$1$ | $10$ | $n, q \leq 5000$ | |$2$ | $5$ | $q_1 \leq 10$ | |$3$ | $10$ | 所有操作一在所有操作二之前 | |$4$ | $10$ | 所有叶子节点都与根节点距离相同，没有具有一个子节点的节点 | |$5$ | $10$ | 对于所有操作一，$l = r$ | |$6$ | $20$ | 对于所有操作一，$x \in \{-1, 1\}$，每个节点最多有一个子节点 | |$7$ | $10$ | 对于所有操作一，$x \in \{-1, 1\}$ | |$8$ | $10$ | 每个节点最多有一个子节点 | |$9$ | $15$ | 无 | 对于 $100\%$ 的数据，$1 \leq n, q \leq 100000$。