P11143 Strange Cake Game
Background
小 $\mathcal{W}$ 和 小 $\mathcal{M}$ 在 CF 庄园里分蛋糕。
Description
There is a rectangular cake with an area of $n\times m$. Its upper-left vertex is represented as $(0,0)$, and the bottom-right vertex is represented as $(n,m)$.
There are $k$ chocolates on the cake. The position of the $i$-th chocolate is $(x_i-0.5,y_i-0.5)$. **There may be more than one chocolate at the same position.**
Little M and Little W are going to cut the cake with a cake knife. At the very beginning, the knife is positioned at $(0,0)$. Little M and Little W are taking turns to move the knife, with Little W going first. Let's say the knife is at $(x,y)$, and it can be moved to $(x,y+1)$ or $(x+1,y)$ in a turn.
After several turns, the cake will be cut into two parts — the upper-right part belongs to Little W, and the other part belongs to Little W. Both Little W and Little M want to have the most chocolates, so please help them determine: if both of them move the knife optimally, how many chocolates Little W will have.
The following picture shows a cake and a possible way of cutting the cake.

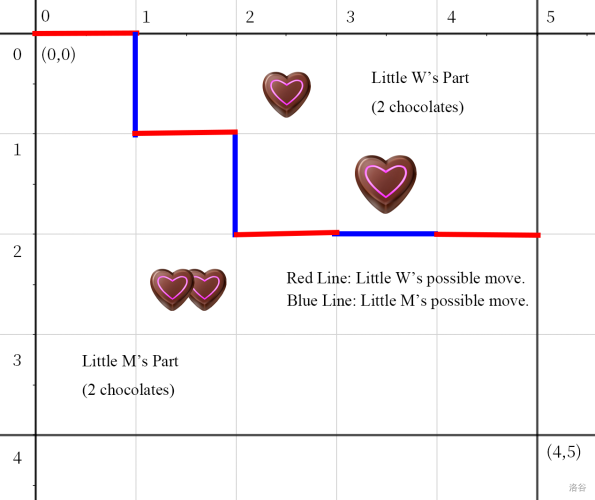
Input Format
The first line contains two integers $n,m$ — the position of the bottom-right vertex of the cake.
The following line contains $k$ — number of the chocolates.
Next $k$ lines, the $i$-th line contains two integers $x_i,y_i$ — the position of $i$-th chocolate is $(x_i-0.5,y_i-0.5)$.
Note that **There may be more than one chocolate at the same position.**
Output Format
A single integer — the number of chocolates that Little W will have if they move the knife optimally.
Explanation/Hint
#### Subtasks and Contraints
- Subtask 1 (5 pts): $n=m=1$;
- Subtask 2 (10 pts): $1 \le n \times m \le 60$;
- Subtask 3 (15 pts): $1 \le n \times m \le 10^5$;
- Subtask 4 (20 pts): $k=1$;
- Subtask 5 (50 pts): No further constraints.
It is guaranteed that
- $0 \le k \le 2 \times 10^5$;
- $1 \le n,m \le 10^{18}$;
- $1 \le x_i \le n$, $1 \le y_i \le m$.