【MX-X6-T4】夢重力

> _空を仰げば$\\$ 青さが僕を$\\$ 飲み込んでしまう気がしてて$\\$ 無重力なら楽だろうか$\\$ 宇宙まで行けたら_ > > _—— [夢重力 - Nanatsukaze](https://music.163.com/#/song?id=2155399298)_ 在天体的随机运转中，如何找到一个没有重力的点呢？

给定一个 $n\times n$ 的网格，其中有 $n$ 个关键点，保证每行每列各有一个关键点。保证 $n$ 是偶数。 我们定义网格中的一个无重力区域为网格的连续的 $\dfrac{n}{2}$ 行和连续的 $\dfrac{n}{2}$ 列构成的大小为 $\dfrac{n}{2}\times \dfrac{n}{2}$ 的子正方形，使得其中不包含任意关键点。 定义 $f(i,j)$ 为交换网格的第 $i$ 行和第 $j$ 行后，不同的无重力区域个数。请对于所有可能的交换求 $f(i,j)$ 的和，即你需要求： $$\sum_{1\leq i<j\leq n}f(i,j)$$ 注意求 $f$ 并不会真正在网格中执行交换，整个过程中不会对网格进行任何修改。

第一行一个整数表示 $n$。保证 $n$ 是偶数。 接下来一行 $n$ 个空格分隔的整数 $p_1,p_2,\dots,p_n$，表示 $n$ 个关键点的位置分别是 $(1,p_1),(2,p_2),\dots,(n,p_n)$。保证 $p$ 是一个排列。

一行一个整数表示答案。

4
1 2 3 4

8

10
9 8 1 10 7 2 4 3 6 5

27

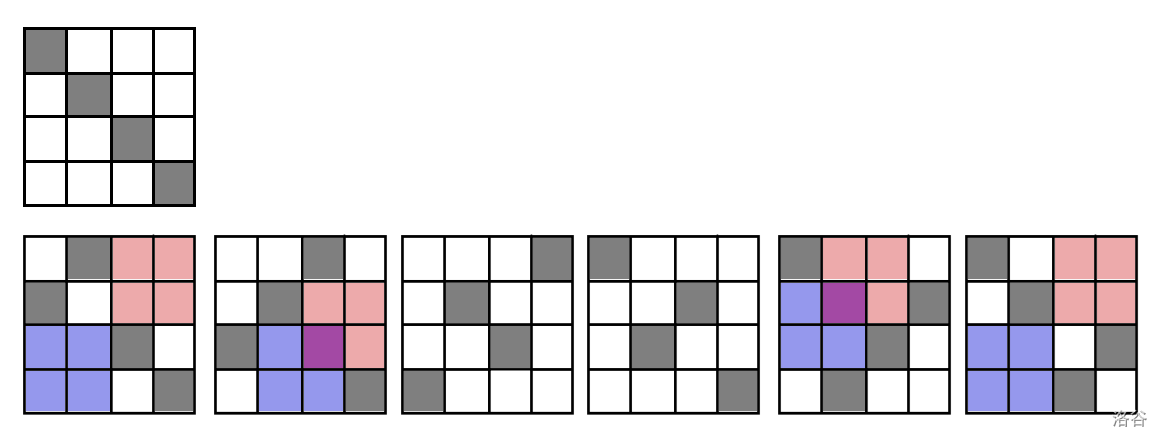
**【样例解释 #1】**  上图中，左上角对应原网格。灰色的部分表示关键点。 下面的 $6$ 个网格分别对应所有可能的交换产生的网格（依次为交换 $(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)$），并使用红色和蓝色标出存在的无重力区域（紫色的位置表示两个无重力区域的交）。不难看出答案为 $2+2+0+0+2+2=8$。 **【数据范围】** 对于所有数据，保证 $2\leq n\leq 2\times 10^5$ 且 $n$ 是偶数，保证 $p$ 是一个排列。 **捆绑测试**，共 4 个 Subtask，具体限制如下所示： - Subtask 1（12 pts）：$n\leq 10$； - Subtask 2（19 pts）：$n\leq 200$； - Subtask 3（34 pts）：$n\leq 2000$； - Subtask 4（35 pts）：无特殊限制。