P11163 [BalkanOI 2023] Weights

**译自 [BalkanOI 2023](https://boi2023.zotks.si) Day1 T2「[Weights](https://boi2023.zotks.si/wp-content/uploads/day_1/d1_weights/en_EN.pdf)」** 给你 $N$ 个天平，每个天平有两个质量可以忽略不计的盘子。天平用从 $1$ 到 $N$ 的整数编号。每个盘子上要么放着另一个天平，要么放着一个质量不可忽略的砝码。编号为 $1$ 的天平放在地上，其他的天平都放在某个天平的盘子上。一共有 $N+1$ 个砝码。砝码用 $1$ 到 $N+1$ 的整数编号，每个砝码的质量用 $N+1$ 个整数 $w_{1}, w_{2} \cdots, w_{N+1}$ 表示。 下图给出了一个由三个天平和四个砝码组成的例子。正体字的数字表示天平和砝码的编号，斜体字的数字表示砝码的质量。例如，编号为 $2$ 的天平放在编号为 $1$ 的天平的左盘上，编号为 $2$ 质量为 $6$ 的砝码放在编号为 $1$ 的天平的右盘上。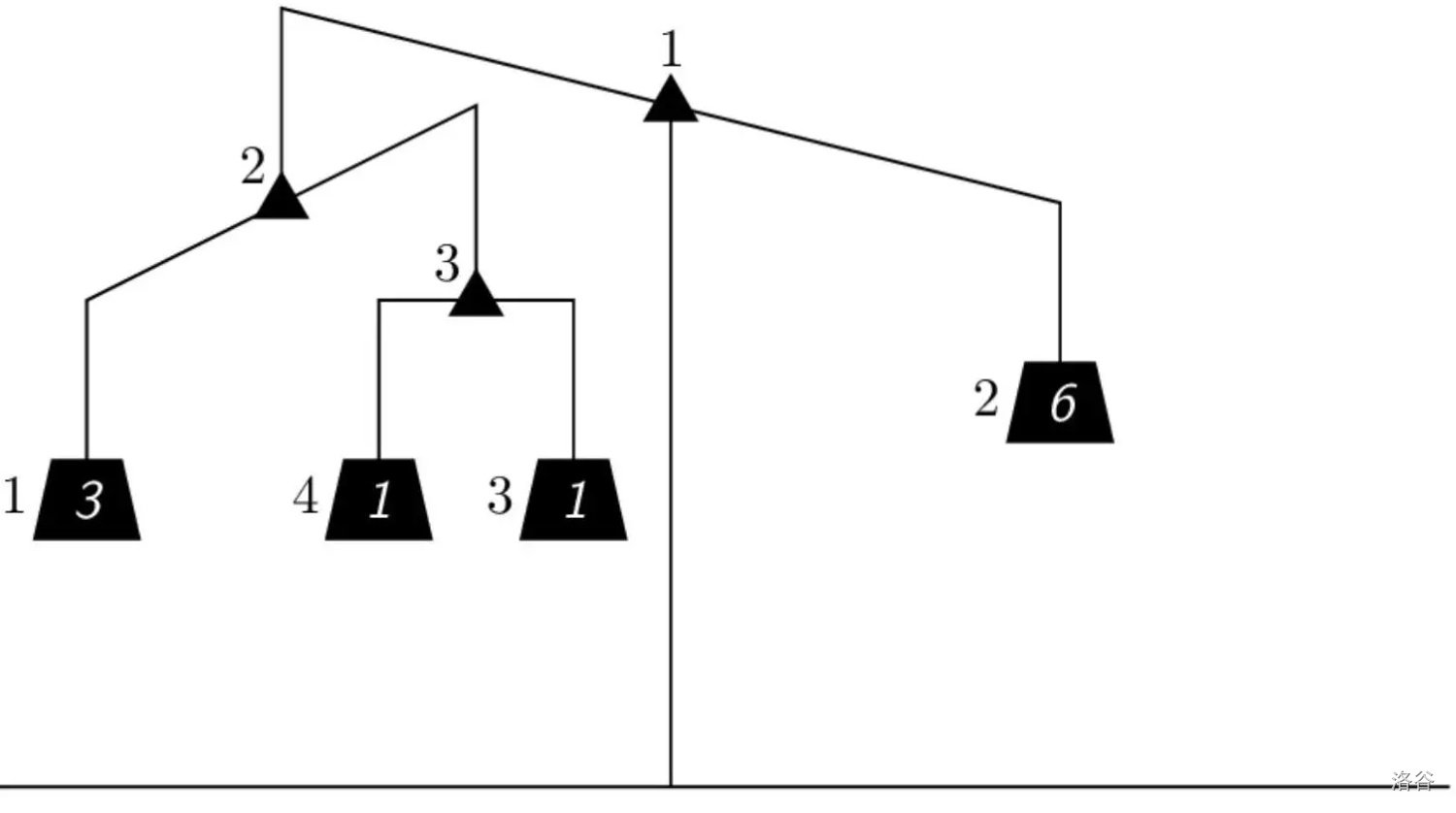  如果一个天平的左盘和右盘的总质量相等，我们说它是平衡的。如果一个天平是平衡的，并且它的两个盘子上要么都是超平衡的天平，要么都是砝码，我们说它是超平衡的。 在上图中，只有天平 $3$ 是平衡的（也是超平衡的），但是如果我们把砝码 $3$ 和 $4$ 的质量都增加到 $1.5$，那么三个天平都会变成超平衡的。然而，如果我们把砝码 $1$ 的质量增加到 $4$，天平 $1$ 会变成平衡的但不是超平衡的，因为天平 $2$ 仍然不平衡。 现在我们要处理 $Q$ 个两种类型的操作： - $1\,k\,w$ : 把砝码 $k$ 的质量改成整数 $w$。 - $2\,s$ : 假设我们想让天平 $s$ 变成超平衡的。我们可以用魔法把一些砝码变得更重！注意新的质量不一定是整数。要让天平 $s$ 变成超平衡的，天平 $s$ 上的最小总质量是多少？由于这个数可能很大，输出它对 $998244353$ 取模的结果。可以证明在给定的限制下，结果总是一个整数。 注意，类型 $1$ 的操作会改变砝码的质量，而类型 $2$ 的操作不会。

第一行包含两个整数 $N$ 和 $Q$。 接下来的 $N$ 行中的第 $i\ (1\leq i\leq N)$ 行包含两对字符和数字，每对描述了第 $i$ 个天平的一个盘子：字符是 `S`（天平）或 `W`（砝码），表示盘子上的物体的类型，整数是相应物体的编号。保证一个天平永远不会放在一个编号更大的天平上。 接下来的一行包含 $N+1$ 个整数 $w_{1}, w_{2}, \cdots, w_{N+1}$，表示砝码的质量。 最后的 $Q$ 行表示操作。每行要么是形如 $1\,k\,w$ 的，要么是形如 $2\,s$ 的，如问题描述中所述。

对于每个类型 $2$ 的操作，在一行上输出相应的最小质量对 $998244353$ 取模的结果。

### 样例解释 为了让天平 $2$ 变成超平衡的，我们把砝码 $3$ 和 $4$ 的质量都增加到 $1.5$。这样，天平 $2$ 和 $3$ 都会变成平衡的，因此 $2$ 也就是超平衡的。天平 $2$ 上的总质量是 $3+1.5+1.5=6$。当我们这样做的时候，天平 $1$ 也会变成平衡的，所以它也是超平衡的，它的总质量是 $6+3+1.5+1.5=12$。当我们把砝码 $3$ 的质量改成 $2$ 的时候，这种方法就不行了。因此，为了让天平 $1$ 变成超平衡的，我们可以把砝码 $1$ 的质量改成 $4$，砝码 $2$ 的质量改成 $8$，砝码 $4$ 的质量改成 $2$。这样，天平 $1$ 上的总质量就是 $8+4+2+2=16$。 ### 数据范围 对于所有输入数据，满足： - $1 \leq N \leq 2 \cdot 10^{5}$ - $1 \leq Q \leq 2 \cdot 10^{5}$ - $1 \leq w_{i} \leq 10^{9}$ - 对于每个类型 $1$ 的操作：$1 \leq k \leq N+1$ - 对于每个类型 $1$ 的操作：$1 \leq w \leq 10^{9}$ - 对于每个类型 $2$ 的操作：$1 \leq s \leq N$ 详细子任务附加限制及分值如下表所示。令砝码的深度表示它直接或间接所在的盘子的数量。 | 子任务编号 | 附加限制 | 分值 | | :--: | :--: | :--: | | $1$ | 每个天平的至少一个盘子上有砝码 | $9$ | | $2$ | 每个砝码的深度相同 | $8$ | | $3$ | 每个砝码的深度小于 $30$，且 $N, Q \leq 5000$ | $24$ | | $4$ | 每个砝码的深度小于 $30$ | $14$ | | $5$ | $N, Q \leq 5000$ | $14$ | | $6$ | 无附加限制 | $31$ |