P11167 [BalkanOI 2023] Aliens

**译自 [BalkanOI 2023](https://boi2023.zotks.si) Day2 T3「[Aliens](https://boi2023.zotks.si/wp-content/uploads/day_2/d2_aliens/en.pdf)」** 马里博尔刚刚被外星人拜访了！他们与你分享了他们的技术和历史。 有 $N+1$ 个行星，从 $0$ 到 $N$ 编号，地球的编号为 $N$。每个行星都有一个唯一的人口数 $P_{i}\ (0\leq i\leq N)$。行星之间用 $N$ 个双向传送门连接，你可以只用这些传送门在任意两个行星之间旅行。传送门 $i$（$0\leq i\leq N-1$）连接了行星 $U_{i}$ 和 $V_{i}$。两个行星之间的距离是旅行所需的最少传送门数。 你从地球出发，想要去游览 $K$ 个其他行星 $A_{0}, A_{1}, \ldots, A_{K-1}$。这些被称为**起源行星**。每个起源行星和地球只有一个传送门连接。你的旅程为从地球出发，访问所有起源行星以及沿途所有行星的最短路线。令 $S$ 为所有访问过的行星的集合。 现在，外星人决定通过向你提问 $Q$ 个以下两种类型的问题来测试地球是否有资格加入他们的超级文明： - 类型 $1$：集合 $S$ 的大小是多少？ - 类型 $2$：他们从 $S$ 中选出一个行星 $x$，一个距离 $d$，和一个数字 $r$。他们问你，在距离 $x$ 为 $d$ 的行星中，按人口数从小到大排列的第 $r$ 个行星是哪个。（例如，如果 $r=1$ 答案就是距离 $x$ 为 $d$ 的星球中人口数最少的行星。这个行星可以也可以不属于集合 $S$。） 只有一个类型 $1$ 的查询。

第一行包含三个整数 $N, K, Q$。 第二行包含 $N+1$ 个整数 $P_{0}, \ldots, P_{N}$。 第三行包含 $K$ 个整数 $A_{0}, \ldots, A_{K-1}$。 接下来的 $N$ 行中的第 $i\ (1\leq i\leq N-1)$ 行包含两个整数 $U_{i}$ 和 $V_{i}$。 接下来的 $Q$ 行满足以下格式之一： - $1$ 表示一个类型 $1$ 的查询； - $2\,x\,d\,r$ 表示一个类型 $2$ 的查询。

对于每个查询，输出一行。对于类型 $1$ 的查询，输出游览期间访问的行星数；对于类型 $2$ 的查询，输出距离 $x$ 为 $d$ 的行星中按人口数排列的第 $r$ 个行星。

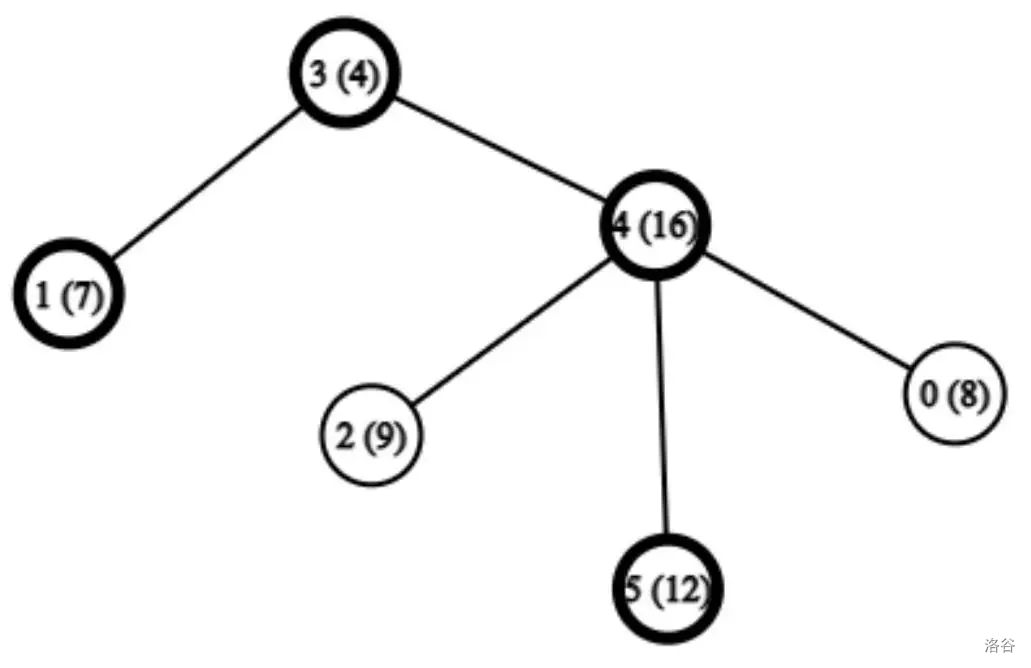
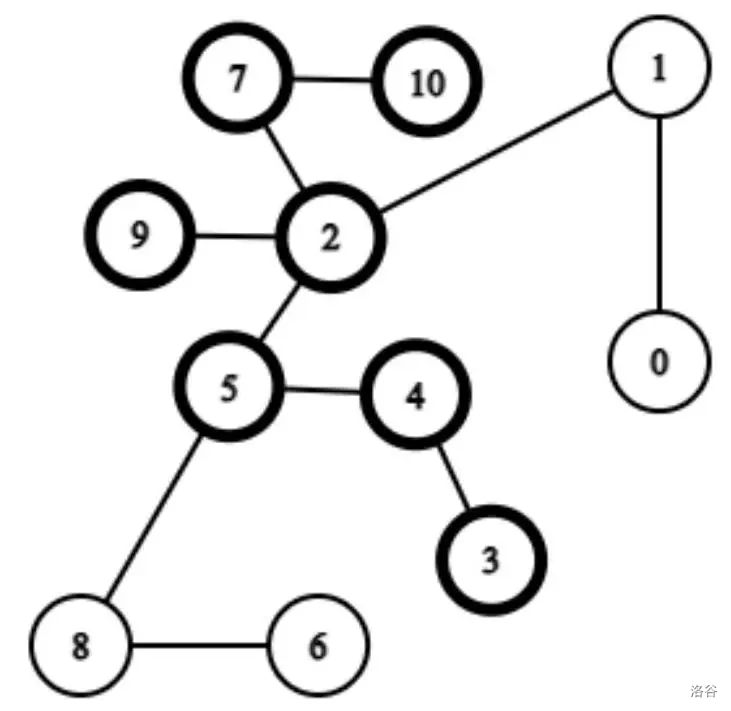
### 样例 1 解释  只有一个起源行星，我们在游览中访问了行星 $S=\{1,3,4,5\}$。类型 $2$ 的查询有： - $x=4, d=2, r=1$ - 距离行星 $4$ 为 $2$ 的只有行星 $1$。 - $x=3, d=2, r=1$ - 距离行星 $3$ 为 $2$ 的有行星 $0,2,5$。其中，行星 $0$ 的人口数最少。 - $x=4, d=1, r=3$ - 距离行星 $4$ 为 $1$ 的有行星 $0,2,3,5$，它们按人口数的顺序是 $3,0,2,5$。其中第三个是行星 $2$。 - $x=5, d=2, r=3$ - 距离行星 $5$ 为 $2$ 的有行星 $0,2,3$，它们按人口数的顺序是 $3,0,2$。其中第三个是行星 $2$。 ### 样例 2 解释  ### 数据范围 对于所有输入数据，满足： - $1 \leq N \leq 10^5$ - $1 \leq K \leq 10$ - $1 \leq Q \leq 10^5$ - $1 \leq P_{i} \leq 10^{9}\ (0 \leq i \leq N)$； - 所有的 $P_{i}$ 都是不同的 - $0 \leq A_{i} \leq N-1\ (0 \leq i \leq K-1)$ - $0 \leq U_{i}, V_{i} \leq N\ (0 \leq i \leq N-1)$ - $K$ 个起源行星和地球只有一个传送门连接 - 对于每个类型 $2$ 的查询，满足 $x \in S, d \geq 1$，且 $r \geq 1$ - 保证距离 $x$ 为 $d$ 的行星至少有 $r$ 个 详细子任务附加限制及分值如下表所示。 | 子任务编号 | 附加限制 | 分值 | | :--: | :--: | :--: | | $1$ | $Q=1$ | $3$ | | $2$ | $N \leq 2000, Q \leq 2000$ | $14$ | | $3$ | $K=1$ | $21$ | | $4$ | $N \leq 10000$ | $12$ | | $5$ | $Q \leq 10000$ | $13$ | | $6$ | 无附加限制 | $37$ |