P11174 「CMOI R1」Looking For Edge Of Ground／City Planning
题目背景
[如何对 $n$ 个点的简单有标号无向连通图计数？](https://www.luogu.com.cn/problem/P4841)$\small\color{white}/42^{\text{nd}}\text{Problem by ArCu}.$
有一个显然错误的做法：枚举一棵树，然后在上面加边。
你需要求每张图被统计的次数的平方和。
题目描述
给定正整数 $n$。
一开始，$\text{ClBe}$ 会选定一棵 $n$ 个点的有标号无向无根树，将树上的边染成白色。然后他会在这棵树上加任意多条边，且满足：
* 新加的边是黑色的无向边；
* 加完边后的图忽略边的颜色后是一张简单图。
接下来 $\text{ClBe}$ 会将所有可能得到的结果放到一个集合 $S$ 中。
显然这种统计连通图个数的方法会把一个图算很多遍，所以 $\text{ClBe}$ 定义 $f(G)$：$S$ 中有 $f(G)$ 个图在忽略边的颜色后和 $G$ 相同（两个图 $A,B$ 相同指对于任意一条边 $(u,v)$，$(u,v)\in A\iff(u,v)\in B$）。
（$\sum_G$ 代表对所有可能的图 $G$ 求和。）显然
$$\sum_{G}f(G)=n^{n-2}2^\binom{n-1}2$$
所以你需要求
$$\sum_{G}f(G)^2$$
答案对 $998244353$ 取模。很可惜因为一些原因模数**不能**取 $1004535809$。
输入格式
无
输出格式
无
说明/提示
$\text{Sample Explanation}:$
集合 $S$ 中包含以下 $6$ 张图（边权为 $0$ 代表白边，为 $1$ 代表黑边，点的编号为 $1A$ 代表这是图 $A$ 的 $1$ 号点）：
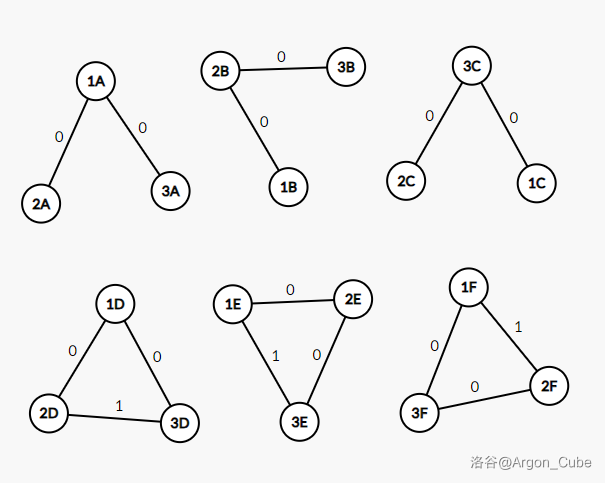
$3$ 个点的连通图有 $4$ 种：
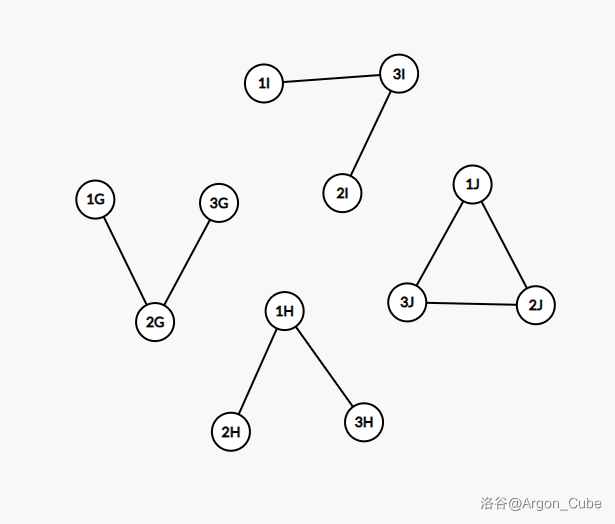
忽略颜色后，
* 与 $G$ 相同的有 $B$；
* 与 $H$ 相同的有 $A$；
* 与 $I$ 相同的有 $C$；
* 与 $J$ 相同的有 $D,E,F$；
答案为 $f(G)^2+f(H)^2+f(I)^2+f(J)^2=1^2+1^2+1^2+3^2=12$。
$\text{Details of Subtasks}:$
本题采用捆绑测试。
| $\text{Subtask}$ | $n